


Next: A.2 The Central Limit
Up: A. Basis of the
Previous: A. Basis of the
A normal distribution in a variateA.1 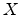 with mean
with mean
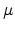 and variance
and variance 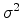 is a statistic distribution with the
probability function
is a statistic distribution with the
probability function
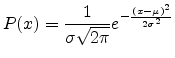 |
(A.1) |
on the domain
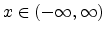 .
.
DEMOIVRE developed the normal distribution as an approximation to the
binomial distribution, and it was subsequently used by LAPLACE in
1783 to study measurement errors and by GAUSS in 1809 in the
analysis of astronomical data.
The so-called ``standard normal distribution'' is given by taking 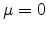 and
and
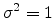 in a general normal distribution. An arbitrary normal
distribution can be converted to a standard normal distribution by changing
variables to
in a general normal distribution. An arbitrary normal
distribution can be converted to a standard normal distribution by changing
variables to
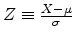 , so
, so
 ,
yielding
,
yielding
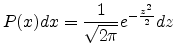 |
(A.2) |
The normal distribution function 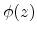 gives the probability that a
standard normal variate assumes a value in the interval
gives the probability that a
standard normal variate assumes a value in the interval ![$ [0,z]$](img337.png) ,
,
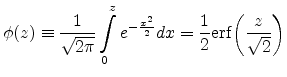 |
(A.3) |
where 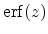 is the error function. Neither
is the error function. Neither
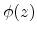 nor
nor 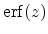 can be expressed in terms of finite additions,
subtractions, multiplications, and root extractions, and so both must be
either computed numerically or otherwise approximated.
can be expressed in terms of finite additions,
subtractions, multiplications, and root extractions, and so both must be
either computed numerically or otherwise approximated.
The normal distribution is the limiting case of a discrete binomial
distribution 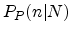 as the sample size N becomes large, in which case
as the sample size N becomes large, in which case
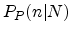 is normal with mean and variance
is normal with mean and variance
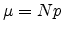 |
(A.4) |
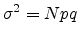 |
(A.5) |
with
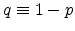 .
.
The distribution 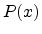 is properly normalized since
is properly normalized since
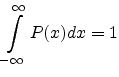 |
(A.6) |
The cumulative distribution function which gives the probability that a
variate will assume a value 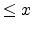 , is then the integral of the normal
distribution
, is then the integral of the normal
distribution
The normal distribution function is obviously symmetric about 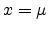
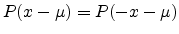 |
(A.8) |
and its maximum value is situated at 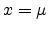
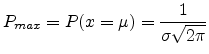 |
(A.9) |
Normal distributions have many convenient properties, so random variates with
unknown distributions are often assumed to be normal, especially in physics
and astronomy. Although this can be a dangerous assumption, it is often a good
approximation due to a surprising result known as the central limit theorem
(see next section).
Among the amazing properties of the normal distribution are that the normal
sum distribution and normal difference distribution obtained by respectively
adding and subtracting variates 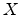 and
and 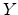 from two independent normal
distributions with arbitrary means and variances are also normal. The normal
ratio distribution obtained from
from two independent normal
distributions with arbitrary means and variances are also normal. The normal
ratio distribution obtained from
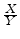 has a Cauchy distribution.
has a Cauchy distribution.
The unbiased estimatorA.2 for the
variance of a normal distribution is given by
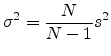 |
(A.10) |
where
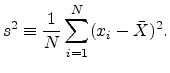 |
(A.11) |
The characteristic function for the normal distribution is
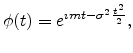 |
(A.12) |
and the moment-generating function is
so
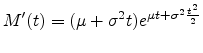 |
|
![$\displaystyle M''(t) = \left[\sigma^2 + (\mu + t \sigma^2)^2\right] e^{\mu t + \sigma^2 \frac{t^2}{2}}$](img365.png) |
(A.14) |
Footnotes
- ... variateA.1
- A variate is a generalization of
the concept of a random variable that is defined without reference to a
particular type of probabilistic experiment. It is defined as the set of all
random variables that obey a given probabilistic law. It is common practice
to denote a variate with a capital letter (most commonly X).
- ... estimatorA.2
- An estimator
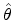 is an unbiased
estimator of
is an unbiased
estimator of 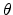 if
if
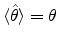 .
.



Next: A.2 The Central Limit
Up: A. Basis of the
Previous: A. Basis of the
R. Minixhofer: Integrating Technology Simulation
into the Semiconductor Manufacturing Environment
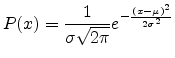
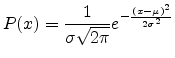
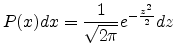
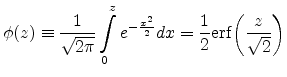
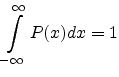
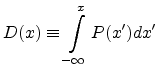
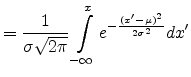
![$\displaystyle = \frac{1}{2}\left[1+\erf {\left(\frac{x-\mu}{\sigma \sqrt{2}}\right)}\right]$](img349.png)
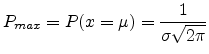
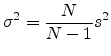
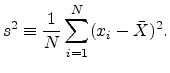
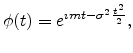
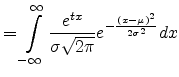
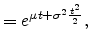
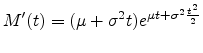
![$\displaystyle M''(t) = \left[\sigma^2 + (\mu + t \sigma^2)^2\right] e^{\mu t + \sigma^2 \frac{t^2}{2}}$](img365.png)