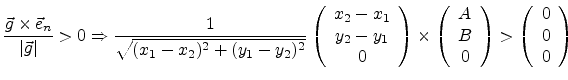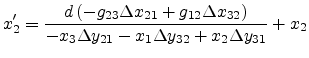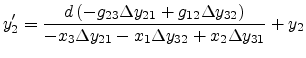


Next: D. From Boltzmann Distribution
Up: Dissertation Rainer Minixhofer
Previous: B.4 Electron Beam Exposure
C. General Algorithm for Polygon-Biasing
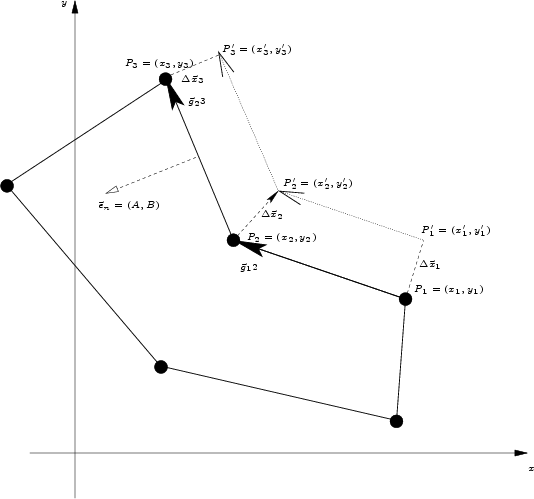
The situation for biasing a polygon is sketched in
Figure C.1. A polygon is defined as a sequence of points
which are given in a counterclockwise order by oriented segments (vectors).
A general algorithm to calculate a new ``shrinked'' or ``grown'' polygon based
on shifting its segments parallel by a certain amount (the bias) has to be applied.
This shift is equivalent to the movement of the points of the polygon by a
normal vector 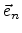 calculated from the normal vectors of the two
segments
calculated from the normal vectors of the two
segments 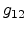 and
and 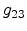 times the bias.
times the bias.
This algorithm is only valid for convex polygons. For concave polygons
(polygons where at least one point has an internal angle
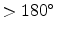 ) this
algorithm may fail because of point collisions or generation of
loops. However, for small bias and suitable geometries the following simple
algorithm is applicable.
) this
algorithm may fail because of point collisions or generation of
loops. However, for small bias and suitable geometries the following simple
algorithm is applicable.
Figure C.1:
Geometrical situation when biasing a polygon with a given distance
 |
The line segment 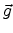 can be described by the general parametric line
equation:
can be described by the general parametric line
equation:
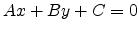 |
(C.1) |
Furthermore, the normal vector 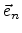 is given by
is given by
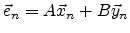 |
(C.2) |
and thus the second equation
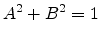 |
(C.3) |
must be fulfilled too. Substituting the start and end coordinates of the
vector
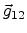 ,
,
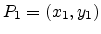 and
and
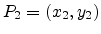 into
(C.1) and (C.3) gives three equations which
have to be solved to get the parameters
into
(C.1) and (C.3) gives three equations which
have to be solved to get the parameters 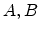 of the line segment.
of the line segment.
with the solutions
Per definition the normal vector 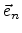 is positive if the line segment
is positive if the line segment
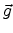 is rotated
is rotated 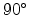 counterclockwise into the normal vector. This
means
counterclockwise into the normal vector. This
means
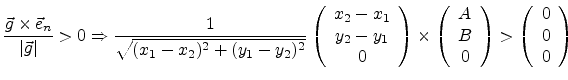 |
(C.9) |
which yields the criteria
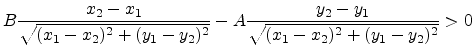 |
(C.10) |
The relation (C.11) is only fulfilled with the solution
of the (C.8),(C.9).
To determine the vector by which each point is shifted during biasing (by the
distance d), the two
line segments
 and
and
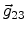 attached to the point are moved
parallel and thus form the new intersection point
attached to the point are moved
parallel and thus form the new intersection point 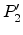 . The normal vectors
remain the same, but the parameters
. The normal vectors
remain the same, but the parameters 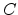 of the general line equations change
accordingly to the parallel shift. The initial intersection
point
of the general line equations change
accordingly to the parallel shift. The initial intersection
point
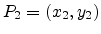 is moved by the vector
is moved by the vector
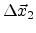 to the point
to the point
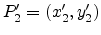 (see Figure C.1). The parameters
(see Figure C.1). The parameters
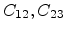 of the shifted line equations are calculated from their respective
line equations and the unchanged line parameters
of the shifted line equations are calculated from their respective
line equations and the unchanged line parameters
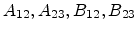 .
.
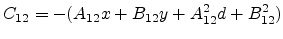 |
(C.13) |
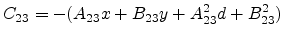 |
(C.14) |
The new intersection point
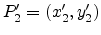 must satisfy both line equations and thus by
solving the equations the new intersection point coordinates yield
must satisfy both line equations and thus by
solving the equations the new intersection point coordinates yield
Substituting (C.12),(C.13) in
(C.17),(C.18) and using the
substitutions
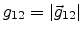 ,
,
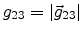 ,
,
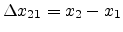 ,
,
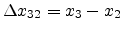 ,
,
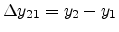 and
and
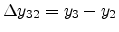 gives finally
gives finally
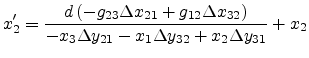 |
(C.17) |
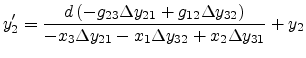 |
(C.18) |



Next: D. From Boltzmann Distribution
Up: Dissertation Rainer Minixhofer
Previous: B.4 Electron Beam Exposure
R. Minixhofer: Integrating Technology Simulation
into the Semiconductor Manufacturing Environment

![]() can be described by the general parametric line
equation:
can be described by the general parametric line
equation: