|
|
|
|
Dissertation Martin Wagner | Previous: 3.5.1 Microscopic and Macroscopic Quantities Up: 3.5 Macroscopic Transport Models Next: 3.5.3 A Hierarchy of Transport Models |
The basic idea behind the method of moments is not to solve the Boltzmann transport equation coupled with the Poisson equation directly, but to derive a set of balance and flux equations for macroscopic quantities based on the moments of the Boltzmann transport equation. Theoretically, an arbitrary number of equations can be derived, each containing information from the next-higher equation. As a consequence, the number of variables exceeds the number of equations. In order to obtain a closed equation system, the derivation of moments has to be truncated and a closure relation has to be formulated by a suitably chosen ansatz [81,82] based on the information incorporated in the underlying lower moments equations. Besides several theoretical approaches [83], the closure can be obtained by extraction of the missing next-higher moment from Monte-Carlo simulations [84].
In order to obtain a certain moment equation, the Boltzmann transport equation is multiplied by a
general weight function and integrated over
![]() -space according to
equations (3.19) and (3.20). Thereby, the series of weight functions is
chosen as the powers of increasing orders of the momentum
-space according to
equations (3.19) and (3.20). Thereby, the series of weight functions is
chosen as the powers of increasing orders of the momentum
![]() . Because of
this average in
. Because of
this average in
![]() -space, information on the distribution of microscopic
quantities over the momentum is lost, which is originally incorporated in
Boltzmann's equation. However, the information incorporated in the
macroscopic equations is sufficient for a wide range of engineering
applications.
-space, information on the distribution of microscopic
quantities over the momentum is lost, which is originally incorporated in
Boltzmann's equation. However, the information incorporated in the
macroscopic equations is sufficient for a wide range of engineering
applications.
For scalar-valued weights
![]() , the application of the moment definition to
Boltzmann's equation (3.10) leads to the conservation equation for the
general weight function
, the application of the moment definition to
Boltzmann's equation (3.10) leads to the conservation equation for the
general weight function
![]()
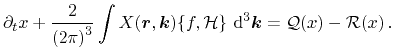 |
(3.26) |
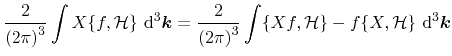 |
(3.27) | ||
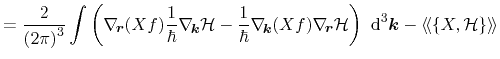 |
|||
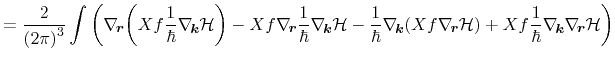 |
|||
M. Wagner: Simulation of Thermoelectric Devices