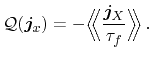3.5.4 Relaxation Time Approximation
In order to obtain an expression for the right hand side of (3.29)
that can be handled analytically, a commonly used simplification -- the
relaxation time approximation is introduced [73]. For small
deviations of the distribution function
 from its equilibrium state
from its equilibrium state
 ,
the collision term can be expressed by [79]
,
the collision term can be expressed by [79]
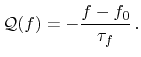 |
(3.31) |
Within this formulation, the distribution function
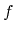 relaxes to its
equilibrium state
relaxes to its
equilibrium state
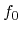 with the time constant
with the time constant
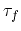 after removing all
driving forces.
after removing all
driving forces.
The moments of the collision term can be modeled following different
strategies. Bløtekjær proposed a set of one single relaxation time for each
macroscopic moment derived [88], thus the according formulations
read
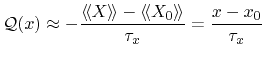 |
|
|
(3.32) |
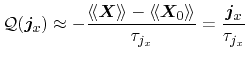 |
|
|
(3.33) |
for macroscopic balance and flux equations, respectively. In equilibrium, all
averages of vector-valued weights vanish, thus
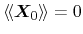 . The
relaxation times
. The
relaxation times
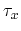 and
and
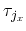 are generally dependent on the
distribution function and represent the parameters of the transport model. In
order to gain accurate results, they have to be carefully calibrated. However,
only the particle flux relaxation time, which is connected to the carrier
mobility is accessible by measurement. Models for all other relaxation times
can be extracted from Monte-Carlo simulations, which incorporate information
on the full distribution function. In order to obtain a closed formulation of
the transport model, the relaxation times have to be modeled with respect to
quantities available in the macroscopic transport model.
are generally dependent on the
distribution function and represent the parameters of the transport model. In
order to gain accurate results, they have to be carefully calibrated. However,
only the particle flux relaxation time, which is connected to the carrier
mobility is accessible by measurement. Models for all other relaxation times
can be extracted from Monte-Carlo simulations, which incorporate information
on the full distribution function. In order to obtain a closed formulation of
the transport model, the relaxation times have to be modeled with respect to
quantities available in the macroscopic transport model.
In contrast to the macroscopic relaxation time approximation applied in
Bløtekjær's approach, Stratton's ansatz incorporates one microscopic relaxation
time
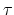 for the entire transport model that describes the scattering of
single carriers. Therefrom, the according formulation for the collision term
reads
for the entire transport model that describes the scattering of
single carriers. Therefrom, the according formulation for the collision term
reads
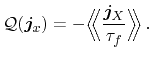 |
(3.34) |
The weights for the odd moment equations are chosen in a way that the right
sides become the fluxes themselves. As a consequence, additional terms in the
flux equations appear, which are systematically derived and analyzed in the
sequel. The relaxation time
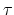 is often modeled to depend on the energy
by a power law
is often modeled to depend on the energy
by a power law
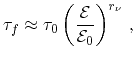 |
(3.35) |
which enables the analytical treatment of several integrals. Depending on the
dominant scattering mechanism, the scattering parameter
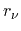 takes values
between
takes values
between 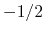 for acoustic phonon scattering and
for acoustic phonon scattering and 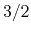 for ionized impurity
scattering. While expression (3.35) is valid with a constant
for ionized impurity
scattering. While expression (3.35) is valid with a constant
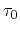 for acoustic phonon scattering,
for acoustic phonon scattering,
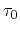 is slightly energy dependent
for ionized impurity scattering [73].
is slightly energy dependent
for ionized impurity scattering [73].
M. Wagner: Simulation of Thermoelectric Devices
![]() from its equilibrium state
from its equilibrium state
![]() ,
the collision term can be expressed by [79]
,
the collision term can be expressed by [79]
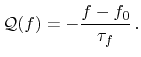
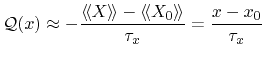
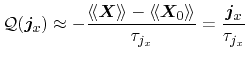
![]() for the entire transport model that describes the scattering of
single carriers. Therefrom, the according formulation for the collision term
reads
for the entire transport model that describes the scattering of
single carriers. Therefrom, the according formulation for the collision term
reads