next up previous contents
Next: 5.3.2 Assembling Up: 5.3 Two-Dimensional Vector Finite Previous: 5.3 Two-Dimensional Vector Finite   Contents

5.3.1 Linear Vector Shape Functions on a Triangular Elements

The following in this subsection refers to the triangular element from (Fig. <4.1>). The field in the element is interpolated similarly as for the three-dimensional case by edge functions. Since there are three edges in the triangular element three interpolation functions are given

$\displaystyle \vec{N}^e_{12} = l_{12}(\lambda^e_1\vec{\nabla}\lambda^e_2 - \lambda^e_2\vec{\nabla}\lambda^e_1)$ (5.76)

$\displaystyle \vec{N}^e_{23} = l_{23}(\lambda^e_2\vec{\nabla}\lambda^e_3 - \lambda^e_3\vec{\nabla}\lambda^e_2)$ (5.77)

$\displaystyle \vec{N}^e_{31} = l_{31}(\lambda^e_3\vec{\nabla}\lambda^e_1 - \lambda^e_1\vec{\nabla}\lambda^e_3).$ (5.78)

The same properties as for the three-dimensional vector element functions can be proved for the two-dimensional ones. Without loss of generality Edge $ 12$ is used to prove the properties of the edge functions. The divergence of a vector edge function is zero, i.e.

$\displaystyle \vec{\nabla}\cdot\vec{N}^e_{12} = l_{12}(\vec{\nabla}\lambda^e_1\... ...{\nabla}\lambda^e_2 - \vec{\nabla}\lambda^e_2\cdot\vec{\nabla}\lambda^e_1) = 0.$ (5.79)

For the rotor of a vector edge function it can be written

$\displaystyle \vec{\nabla}\times\vec{N}^e_{12} = l_{12}(\vec{\nabla}\lambda^e_1... ...bla}\lambda^e_1) = 2l_{12}\vec{\nabla}\lambda^e_1\times\vec{\nabla}\lambda^e_2.$ (5.80)

The tangential component of $ \vec{N}^e_{12}$ on Edge $ 23$ can be obtained from

$\displaystyle \vec{N}^e_{12}\cdot\vec{r}_{23} = (\lambda^e_1\vec{r}_{23})\cdot\vec{\nabla}\lambda^e_2 - \lambda^e_2(\vec{r}_{23}\cdot\vec{\nabla}\lambda^e_1).$ (5.81)

Since $ \lambda^e_1$ vanishes on the Edge $ 23$ and $ \vec{\nabla}\lambda^e_1$ is perpendicular to $ \vec{r}_{23}$ , the two terms on the right hand side of (5.81) are zero and $ \vec{N}^e_{12}$ has no tangential component on the Edge $ 23$ :

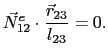$\displaystyle \vec{N}^e_{12}\cdot\frac{\vec{r}_{23}}{l_{23}} = 0.$    

Analogously it can be shown that $ \vec{N}^e_{12}$ has no tangential component on Edge $ 31$ as well. For $ \vec{N}^e_{12}$ along the direction of Edge $ 12$ the following expression is applied

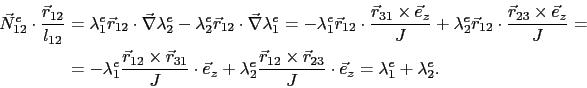\begin{displaymath}\begin{split}\vec{N}^e_{12}\cdot\frac{\vec{r}_{12}}{l_{12}} &... ...{23}}{J}\cdot\vec{e}_z = \lambda^e_1 + \lambda^e_2. \end{split}\end{displaymath}    

Since $ \lambda^e_3$ is zero and therefore $ \lambda^e_1{+}\lambda^e_2$ is one on Edge $ 12$ , the tangential component of $ \vec{N}^e_{12}$ on Edge $ 12$ is one. The vector function $ \vec{H}_{12}$ has a constant tangential component $ \lambda^e_1{+}\lambda^e_2$ only along its corresponding Edge $ 12$ . Along the remaining edges this function does not have a tangential component. Similarly this characteristics applies also to the remaining functions $ \vec{H}_{23}$ and $ \vec{H}_{31}$ . Hence it follows that in an approach of the kind

$\displaystyle \vec{f}(r) = c_1\vec{N}^e_{12} + c_2\vec{N}^e_{23} + c_3\vec{N}^e_{31}$    

the arbitrary coefficients $ c_1$ , $ c_2$ and $ c_3$ are to be regarded as values of the projection of $ \vec{f}(r)$ in the possible edge directions, respectively. This fact justifies the name edge function or edge element.

It is not simple to imagine, how the edge functions look like. The edge function $ \vec{N}^e_{12}$ is visualized in Fig. <5.8>. Fig. <5.9> depicts function $ \vec{f}(r)$ for all coefficients set to one.

Figure 5.8: The shape function along Edge $ 12$ .
\includegraphics[width=0.9\textwidth]{figures/vectorfem2d/shapefunc/N12.eps}

Figure 5.9: The sum of the shape functions in the triangle.
\includegraphics[width=0.9\textwidth]{figures/vectorfem2d/shapefunc/all.eps}

next up previous contents
Next: 5.3.2 Assembling Up: 5.3 Two-Dimensional Vector Finite Previous: 5.3 Two-Dimensional Vector Finite   Contents
A. Nentchev: Numerical Analysis and Simulation in Microelectronics by Vector Finite Elements