



Next: 1.4 TCAD for Electromigration
Up: 1.3 Empirical and Semi-Empirical
Previous: 1.3.2 Resistance Increase and
As already pointed out, the lognormal distribution generally provides a good fit to EM lifetimes [22].
The mean time to failure and the standard deviation of a lognormal distribution are calculated, respectively, by
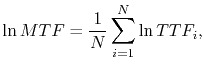 |
(1.17) |
and
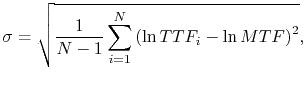 |
(1.18) |
where 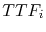 is the time to failure of the
is the time to failure of the 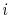 -th test structure and
-th test structure and 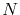 is the number of test structures.
The cumulative failure frequency of the
is the number of test structures.
The cumulative failure frequency of the 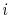 -th structure is given by [19]
-th structure is given by [19]
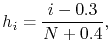 |
(1.19) |
which is then sorted in ascending order of failure times and presented in a probability plot.
The probability density function (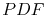 ) of the logonormal distribution has the form
) of the logonormal distribution has the form
![$\displaystyle PDF(t)=\frac{1}{\sigma t\sqrt{2\pi}}\exp\left[-\frac{(\ln t -\ln\symMTF)^2}{2\sigma^2}\right],$](img136.png) |
(1.20) |
and the corresponding cumulative distribution function 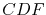 ,
,
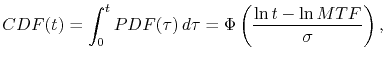 |
(1.21) |
which represents the probability of failure until some defined time 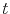 .
Here,
.
Here, 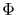 is the integral of the Gaussian function,
is the integral of the Gaussian function,
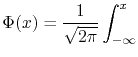 exp exp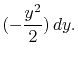 |
(1.22) |
The EM lifetime extrapolation from accelerated tests to operating conditions is based on Black's equation (1.6), and is given by [19,22]
![$\displaystyle TTF_{oper} = \symMTF_{test}\left(\frac{\symCurrDens_{test}}{\symC...
...( \frac{1}{\T_{oper}}-\frac{1}{\T_{test}}\right) + \Phi^{-1}(s)\,\sigma\right],$](img142.png) |
(1.23) |
where 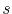 is the cumulative failure percentage accepted at the real operating condition and
is the cumulative failure percentage accepted at the real operating condition and 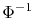 is the inverse function of
is the inverse function of 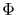 .
The last term in (1.23) is necessary to extrapolate the 50% cumulative failure of the accelerated test to the very small failure percentiles (about 0.01%) allowed under operating conditions [20].
.
The last term in (1.23) is necessary to extrapolate the 50% cumulative failure of the accelerated test to the very small failure percentiles (about 0.01%) allowed under operating conditions [20].
Note that this extrapolation procedure has an exponential dependence on the standard deviation of accelerated lifetimes, which might dominate the failure extrapolation over the mean time to failure. Therefore, in order to increase the interconnect lifetime at use conditions, it is necessary to increase the mean time to failure as well as to reduce the standard deviation (
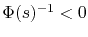 for very small failure percentiles
for very small failure percentiles 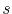 ).
).




Next: 1.4 TCAD for Electromigration
Up: 1.3 Empirical and Semi-Empirical
Previous: 1.3.2 Resistance Increase and
R. L. de Orio: Electromigration Modeling and Simulation
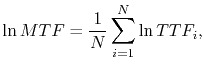
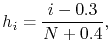
![]() ) of the logonormal distribution has the form
) of the logonormal distribution has the form
![$\displaystyle PDF(t)=\frac{1}{\sigma t\sqrt{2\pi}}\exp\left[-\frac{(\ln t -\ln\symMTF)^2}{2\sigma^2}\right],$](img136.png)
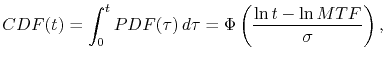
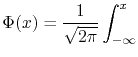 exp
exp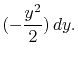
![]() for very small failure percentiles
for very small failure percentiles ![]() ).
).