



Next: 3.3 Electromigration Induced Stress
Up: 3.2 Material Transport Equations
Previous: 3.2.1 Fast Diffusivity Paths
3.2.2 Anisotropic Diffusivity: Diffusion Dependence on Stress
Residual mechanical stresses are introduced on interconnect lines as a result of the fabrication process flow [141]. These stresses can be very high, significantly affecting the diffusion coefficient of the interconnect metal atoms [142].
Typically, the diffusion dependence on stress is taken into account through a simple modification of the usual diffusion coefficient expression (2.10) to [54,97]
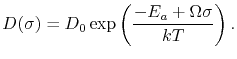 |
(3.13) |
In this way, (3.13) describes the effect of a scalar hydrostatic stress on the scalar diffusion coefficient.
However, Flynn [143] pointed out that, for a homogeneously deformed cubic crystal with strain field
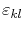 , there is an additional contribution proportional to
, there is an additional contribution proportional to
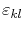 to the diffusion of the form
to the diffusion of the form
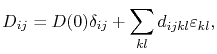 |
(3.14) |
where 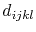 is the elastodiffusion tensor, which can be experimentally determined. Here, the simple scalar diffusivity is replaced by a tensorial quantity. Consequently, in the presence of a stress field the diffusivity can now become anisotropic, depending on the properties of
is the elastodiffusion tensor, which can be experimentally determined. Here, the simple scalar diffusivity is replaced by a tensorial quantity. Consequently, in the presence of a stress field the diffusivity can now become anisotropic, depending on the properties of 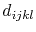 .
.
Based on microscopic lattice theory, Dederichs and Schroeder [142] showed that the diffusivity in a simple face-centered cubic crystal (fcc) follows
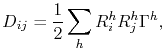 |
(3.15) |
where 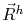 is the jump vector for a hop
is the jump vector for a hop 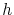 and
and 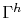 is the corresponding jump rate.
From classical thermodynamics the jump rate is given by [59,144]
is the corresponding jump rate.
From classical thermodynamics the jump rate is given by [59,144]
![$\displaystyle \Gamma^h = \nu\exp\left[-\frac{E_m^h(\boldsymbol\symStrain)}{\kB\T}\right],$](img329.png) |
(3.16) |
where 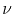 is the Debye frequency (
is the Debye frequency (
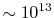 s
s for metals [144]) and
for metals [144]) and 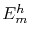 is the migration energy barrier. The presence of an external strain field affects the jump rate by changing the migration energy barrier according to [145]
is the migration energy barrier. The presence of an external strain field affects the jump rate by changing the migration energy barrier according to [145]
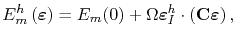 |
(3.17) |
where 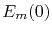 is the migration energy barrier in the absence of an external field,
is the migration energy barrier in the absence of an external field,
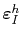 is the induced strain,
is the induced strain,
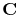 is the elasticity tensor, and
is the elasticity tensor, and
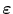 is the applied external strain.
For a fcc crystal the elasticity tensor has the form [146]
is the applied external strain.
For a fcc crystal the elasticity tensor has the form [146]
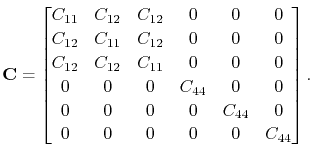 |
(3.18) |
Combining (3.16) and (3.17) one obtains
![$\displaystyle \Gamma^h = \Gamma_0\exp\left[-\frac{\symAtomVol\boldsymbol\symStr...
...}\ensuremath{\cdot}\left(\mathbf{C}\boldsymbol\symStrain\right)}{\kB\T}\right],$](img337.png) |
(3.19) |
with
![$\displaystyle \Gamma_0 = \nu\exp\left[-\frac{E_m(0)}{\kB\T}\right].$](img338.png) |
(3.20) |
Considering a single vacant point defect in a crystal lattice, the local volumetric strain induced by the presence of this vacancy is given by
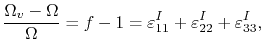 |
(3.21) |
where
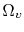 is the vacancy volume and
is the vacancy volume and
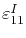 ,
,
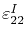 , and
, and
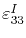 are the induced strains in the given directions. Due to the symmetry of a vacant point defect
are the induced strains in the given directions. Due to the symmetry of a vacant point defect
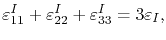 |
(3.22) |
which together with (3.21) yields
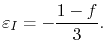 |
(3.23) |
Thus, the induced strain tensor becomes
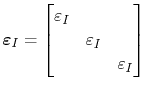 |
(3.24) |
and the induced strain vector is determined by
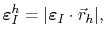 |
(3.25) |
where 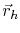 is a jump unit vector for a hop
is a jump unit vector for a hop 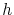 .
.
Normalizing (3.15) with the jump distance 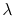 and summing over the
and summing over the 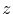 nearest neighbors (
nearest neighbors (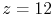 for fcc crystals) one obtains
for fcc crystals) one obtains
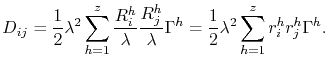 |
(3.26) |
Substituting (3.19) in this equation, the diffusivity tensor in the presence of a external stress field is determined through the expression
![$\displaystyle D_{ij} = \frac{3}{Z}D_0\sum_{h=1}^{z} r_i^h r_j^h \exp\left[-\fra...
...}\ensuremath{\cdot}\left(\mathbf{C}\boldsymbol\symStrain\right)}{\kB\T}\right],$](img351.png) |
(3.27) |
where 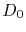 is given by [144]
is given by [144]
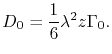 |
(3.28) |
In order to take into account the anisotropy of diffusion, the scalar diffusivity, 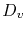 , in the flux equation (3.9) is replaced by the stress dependent diffusivity tensor
, in the flux equation (3.9) is replaced by the stress dependent diffusivity tensor
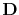 yielding
yielding
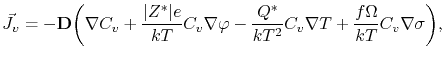 |
(3.29) |
with
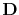 calculated via (3.27).
In this way, the development of mechanical stress can lead to anisotropic diffusion in the interconnect line, therefore, affecting the material transport along the line under electromigration.
calculated via (3.27).
In this way, the development of mechanical stress can lead to anisotropic diffusion in the interconnect line, therefore, affecting the material transport along the line under electromigration.




Next: 3.3 Electromigration Induced Stress
Up: 3.2 Material Transport Equations
Previous: 3.2.1 Fast Diffusivity Paths
R. L. de Orio: Electromigration Modeling and Simulation
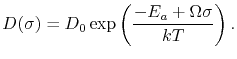
![]() and summing over the
and summing over the ![]() nearest neighbors (
nearest neighbors (![]() for fcc crystals) one obtains
for fcc crystals) one obtains
![]() , in the flux equation (3.9) is replaced by the stress dependent diffusivity tensor
, in the flux equation (3.9) is replaced by the stress dependent diffusivity tensor
![]() yielding
yielding