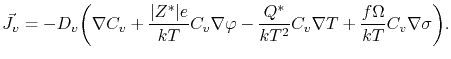3.2 Material Transport Equations

For a proper analysis of the total material transport which occurs in an interconnect line during electromigration, the various driving forces for atomic migration have to be considered. As in copper metallizations atomic migration occurs via vacancy diffusion mechanisms, the total material transport can be equivalently written in terms of vacancies. Thus, the combination of the driving forces leads to the total vacancy flux of the form [53,92]

$$\vec\JV = -\DV \biggl(\ensuremath{\nabla{\CV}} + \frac{\vert\Z\ve... ...symVacRelFactor\symAtomVol}{\kB\T}\CV\ensuremath{\nabla{\symHydStress}}\biggr).$$ (3.9)

In this equation the first term describes a diffusional effect, the second term represents electromigration, the third term represents the material transport which occurs due to thermal gradients in the interconnect, and the last term accounts for the atomic migration caused by gradients of mechanical stress.

Two mechanisms contribute to a local change in vacancy concentration. In the first one vacancies accumulate or vanish due to the existence of flux divergences. In the second, the vacancy concentration is altered by the production or recombination of vacancies in the presence of source/sink mechanisms. Thus, material balance is described by the continuity equation

$$\ensuremath{\ensuremath{\frac{\partial \CV}{\partial t}}} = -\ensuremath{\nabla\cdot{\vec\JV}} + \G,$$ (3.10)

where $\G$ is a function which models vacancy generation and annihilation processes. Vacancy generation or annihilation is related to the change of lattice sites. Therefore, this term is active only at the appropriate interfaces, like grain boundaries and material interfaces [139].