



Next: 4.1.2 Assembly
Up: 4.1 The Finite Element
Previous: 4.1 The Finite Element
4.1.1 Galerkin's Method
Multiplying (4.1) by a function 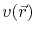 , which is called test or trial function, and integrating over the simulation domain gives the variational formulation
, which is called test or trial function, and integrating over the simulation domain gives the variational formulation
![$\displaystyle \int_{\symDomain} v(\vec r) L[u(\vec r)] d\symDomain = \int_{\symDomain} v(\vec r) f(\vec r) d\symDomain.$](img435.png) |
(4.2) |
Using the notation
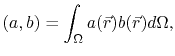 |
(4.3) |
(4.2) can be written as
![$\displaystyle \left(L[u], v\right) = \left(f, v\right).$](img437.png) |
(4.4) |
In order to obtain the corresponding discrete problem, the simulation domain, , is divided in a set of 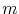 elements,
elements,
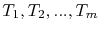 , which do not overlap, i.e.
, which do not overlap, i.e.
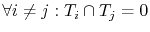 . The mesh obtained by such a domain discretization is represented by
. The mesh obtained by such a domain discretization is represented by
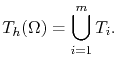 |
(4.5) |
Further, one defines a set 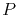 of grid points, also called nodes, with each point
of grid points, also called nodes, with each point 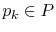 being described by a unique global index
being described by a unique global index
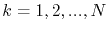 , where
, where 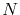 is the total number of grid points in the mesh.
is the total number of grid points in the mesh.
The approximate solution,
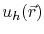 , for the unknown function,
, for the unknown function, 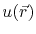 , is given by [152]
, is given by [152]
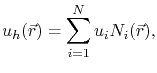 |
(4.6) |
where
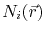 are the so-called basis (or shape) functions. The approximate solution of (4.4) is determined by the coefficients
are the so-called basis (or shape) functions. The approximate solution of (4.4) is determined by the coefficients 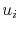 , which represent the value of the unknown function at the node
, which represent the value of the unknown function at the node 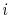 .
At the node
.
At the node 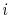 , where the point is given by the coordinates
, where the point is given by the coordinates 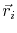 , the basis functions must satisfy the condition
, the basis functions must satisfy the condition
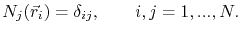 |
(4.7) |
Typically, the basis functions are chosen to be low order polynomials.
Substituting (4.6) in (4.4), and choosing
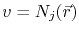 one obtains
one obtains
![$\displaystyle \left(L[\sum_{i=1}^{N} u_iN_i], N_j\right) = \left(f, N_j\right), \qquad j=1,...,N,$](img452.png) |
(4.8) |
and since ![$ L[\cdot]$](img431.png) is a linear operator and the coefficients
is a linear operator and the coefficients 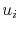 are constants one can write
are constants one can write
![$\displaystyle \sum_{i=1}^{N}u_i\left(L[N_i], N_j\right) = \left(f, N_j\right), \qquad j=1,...,N.$](img453.png) |
(4.9) |
Equation (4.9) is, in fact, a linear system of 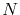 equations with
equations with 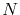 unknowns,
unknowns,
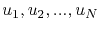 . Thus, it can be written in matrix notation as
. Thus, it can be written in matrix notation as
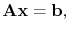 |
(4.10) |
where
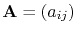 is called stiffness matrix, given by the elements
is called stiffness matrix, given by the elements
![$\displaystyle a_{ij} = \left(L[N_i], N_j\right) = \int_{\symDomain} L[N_i(\vec r)] N_j(\vec r) d\symDomain,\qquad i,j=1,...,N,$](img457.png) |
(4.11) |
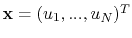 is the vector of unknown coefficients, and
is the vector of unknown coefficients, and
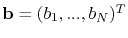 is the load vector, given by
is the load vector, given by
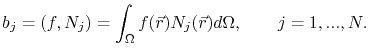 |
(4.12) |




Next: 4.1.2 Assembly
Up: 4.1 The Finite Element
Previous: 4.1 The Finite Element
R. L. de Orio: Electromigration Modeling and Simulation
![]() , which is called test or trial function, and integrating over the simulation domain gives the variational formulation
, which is called test or trial function, and integrating over the simulation domain gives the variational formulation
![]() elements,
elements,
![]() , which do not overlap, i.e.
, which do not overlap, i.e.
![]() . The mesh obtained by such a domain discretization is represented by
. The mesh obtained by such a domain discretization is represented by
![]() , for the unknown function,
, for the unknown function, ![]() , is given by [152]
, is given by [152]
![]() one obtains
one obtains
![]() equations with
equations with ![]() unknowns,
unknowns,
![]() . Thus, it can be written in matrix notation as
. Thus, it can be written in matrix notation as