4.1 The Finite Element Method

Consider the PDE

$$L[u(\vec r)]=f(\vec r),$$ (4.1)

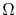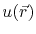defined in a domain $\symDomain$, where $L[\cdot]$ represents a linear differential operator, $u(\vec r)$ is the unknown function to be determined, and 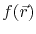$f(\vec r)$ is a given source function. The finite element method consists in discretizing the continuum problem (4.1), so that an approximate solution can be found by solving an algebraic system of equations.

Two main approaches for obtaining the approximate solution are the Ritz method and Galerkin's method [152]. The Ritz method is based on a variational formulation of the PDE, which corresponds to a minimization problem of a functional [152]. Since Galerkin's method allows for more general variational formulations [152], Galerkin's approach is used throughout this work.