


Next: 3.1.2 The Drift-Diffusion Transport
Up: 3.1 Sets of Partial
Previous: 3.1 Sets of Partial
The basic equations solved in a device simulator are the Poisson
equation and the continuity
equations for electrons and holes.
The unknown quantities of this equation system are the electrostatic potential,
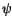 , and the electron and hole concentrations,
, and the electron and hole concentrations, 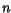 and
and 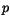 , respectively.
, respectively.
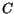 denotes the net concentration of the ionized dopants and other charged
defects,
denotes the net concentration of the ionized dopants and other charged
defects,
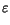 is the dielectric permittivity of the semiconductor, and
is the dielectric permittivity of the semiconductor, and
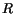 is the net recombination rate.
is the net recombination rate.
Vassil Palankovski
2001-02-28