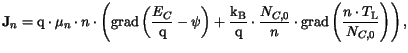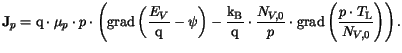


Next: 3.1.3 The Hydrodynamic Transport
Up: 3.1 Sets of Partial
Previous: 3.1.1 The Basic Semiconductor
The drift-diffusion current relations can, amongst
others, be derived from the Boltzmann transport
equation by the method of moments [33] or
from basic principles of irreversible thermodynamics [75]. The
electron and hole current densities are given by
| |
|
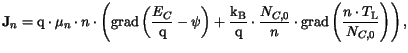 |
(3.4) |
| |
|
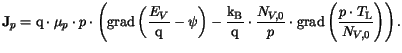 |
(3.5) |
These current relations account for position-dependent
band edge energies, 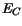 and
and 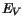 , and for position-dependent effective masses,
which are included in the effective density of states,
, and for position-dependent effective masses,
which are included in the effective density of states, 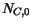 and
and 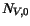 . The
index
. The
index 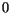 indicates that
indicates that 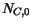 and
and 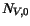 are evaluated at some (arbitrary)
reference temperature,
are evaluated at some (arbitrary)
reference temperature, 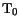 , which is constant in real space
regardless of what the local values of the lattice and carrier temperatures
are.
, which is constant in real space
regardless of what the local values of the lattice and carrier temperatures
are.
Vassil Palankovski
2001-02-28