
Previous: 3.1 Transport Physics Considered for Power Semiconductor Devices Up: 3.1 Transport Physics Considered for Power Semiconductor Devices Next: 3.1.2 Mobility
Computer simulation of semiconductor devices with TCAD tools is attractive because it saves time and lowers the cost to design devices when compared to the experimental approach. In this section the semiconductor transport physics for TCAD environments is described from the viewpoint of power semiconductor devices.
A clear understanding of TCAD is essential to obtain an accurate and reliable simulation result. A great deal of effort has been put into the development of a stable and powerful TCAD tool. In our study MINIMOS-NT, a general purpose device simulator, is used for the simulations.
There are several physical models for the purpose of numerical device simulations starting from Boltzmann's transport equation, Monte-Carlo method, hydrodynamic, and the simple drift-diffusion (including thermodynamic) models. Depending on the type of devices under investigation and the desired accuracy of simulations, one of the physical models above mentioned can be chosen.
The thermodynamic (or non-isothermal) model extends the drift-diffusion
approach to account for electrothermal effects, under the assumption that
the charge carriers are in thermal equilibrium with the lattice.
In this model the electron and hole temperatures ![]() and
and ![]() are given by
are given by
| (3.1) |
where
![]() is the lattice temperature.
is the lattice temperature.
Because the size of power devices is extremely large compared to that of CMOS devices, the drift-diffusion model including thermodynamic effects is usually sufficient in terms of accuracy.
Several assumptions have to be made in order to
derive the drift-diffusion model from the
Boltzmann transport equation (BTE).
In the absence of significant quantum effects and under relatively slow space
and time variations in potential, the transport of carriers in semiconductors
can be expressed through the BTE. The BTE is based on the idea of the carrier distribution
function, ![]() (
(
![]() ), which represents the
probability of finding a carrier at location
), which represents the
probability of finding a carrier at location
![]() with
momentum
with
momentum
![]() at time
at time ![]() .
.
The average values of physical properties associated with carrier transport in semiconductors at any given location in space can be obtained by averaging them over momentum space by taking moments of the distribution function.
The electron concentration
![]() is obtained by integrating the carrier distribution
over momentum space [111,112]
is obtained by integrating the carrier distribution
over momentum space [111,112]
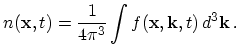 |
(3.2) |
The electron current density is found as
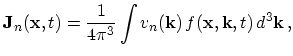 |
(3.3) |
where ![]() (
(
![]() ) is the electron group velocity.
The electron energy
) is the electron group velocity.
The electron energy ![]() is found as
is found as
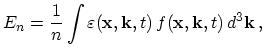 |
(3.4) |
where
![]() is the bands structure for parabolic bands with
is the bands structure for parabolic bands with
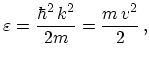 |
(3.5) |
where ![]()
![]()
![]() . We give
. We give
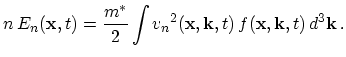 |
(3.6) |
The solution of the BTE along with Maxwell's field equations allows one to numerically simulate the properties of semiconductor devices. However, to obtain a direct solution of the BTE is very difficult and not feasible to device simulations. Balance or conservation equations can be derived to solve these problems.
In particular, the balance equations obtained by taking moments of the BTE present a set of differential equations describing properties such as average carrier density, average momentum, and average carrier energy. These equations can be solved over fairly complex device structures and provide a sufficiently accurate description of carrier transport in most applications. In the majority of simulation studies related to MOS transistors, the effects of magnetic fields can be neglected and the electric field distribution is usually obtained by solving Poisson's equation
| (3.7) |
where
![]() and
and
![]() are the concentrations of ionized donors
and acceptors, respectively.
As shown in (3.2), the zeroth order moment of the electron distribution
function gives the average electron concentration. A momentum balance equation for the
average electron concentration over the simulation domain can be obtained by
taking the corresponding moment of the BTE. This procedure results
in the continuity equations
are the concentrations of ionized donors
and acceptors, respectively.
As shown in (3.2), the zeroth order moment of the electron distribution
function gives the average electron concentration. A momentum balance equation for the
average electron concentration over the simulation domain can be obtained by
taking the corresponding moment of the BTE. This procedure results
in the continuity equations
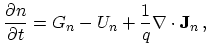 |
(3.8) |
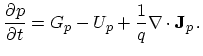 |
(3.9) |
The carrier current densities,
![]() and
and
![]() , are obtained from the
corresponding drift-diffusion equations given by
, are obtained from the
corresponding drift-diffusion equations given by
| (3.10) |
| (3.11) |
In thermal equilibrium in non-degenerate semiconductors, the mobilities are related to the diffusion coefficients through the Einstein relationships
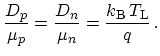 |
(3.12) |
The quantities derived from drift-diffusion equations such as carrier energies and velocities are obtained by averaging over the local carrier distribution and electric fields. Furthermore, the drift-diffusion-based approaches use the Maxwell-Boltzmann distribution for the carrier energies assuming that the carriers are in thermal equilibrium with the lattice.
Jong-Mun Park 2004-10-28