A. First and Second Quantization
In condensed matter physics one is typically concerned with calculating
physical observables from a microscopic description of the system under
consideration. Such microscopic models are usually defined by the
system HAMILTONian 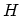 . In many cases of interest the HAMILTONian
takes the form
. In many cases of interest the HAMILTONian
takes the form
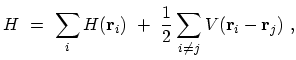 |
(A.1) |
where the first term contains a summation of single-particle HAMILTONians and
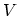 is the interaction potential between particles. The quantity
is the interaction potential between particles. The quantity
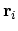 denotes the coordinate of the
denotes the coordinate of the
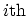 particle, including any discrete
variables such as spin for a system of FERMIons. The summation of
single-particle HAMILTONians by itself is just as simple to solve as each
HAMILTONian alone.
One solves the dynamics of one particle, and the
total properties are the summation of the individual ones. The term which makes
the HAMILTONian hard to solve is the particle-particle interaction
particle, including any discrete
variables such as spin for a system of FERMIons. The summation of
single-particle HAMILTONians by itself is just as simple to solve as each
HAMILTONian alone.
One solves the dynamics of one particle, and the
total properties are the summation of the individual ones. The term which makes
the HAMILTONian hard to solve is the particle-particle interaction
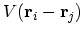 . This term is multiplied by one-half since the
double summation over
. This term is multiplied by one-half since the
double summation over 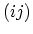 counts each pair twice.
counts each pair twice.
Together with an appropriate number of boundary conditions
the basic problem is the solution of the many-particle
SCHRÖDINGER equation
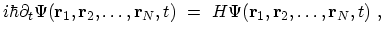 |
(A.2) |
where
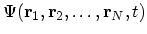 is the many-particle wave
function that in principle contains all relevant information about the state
of the system. One can start by expanding the many-particle wave
function
is the many-particle wave
function that in principle contains all relevant information about the state
of the system. One can start by expanding the many-particle wave
function  in a complete set of symmetrized or anti-symmetrized
products of time-independent single-particle wave functions for Bosons or FERMIons,
respectively [189]. In principle, the
in a complete set of symmetrized or anti-symmetrized
products of time-independent single-particle wave functions for Bosons or FERMIons,
respectively [189]. In principle, the  -body wave function
contains all information, but a direct solution of the SCHRÖDINGER equation
is impractical. Therefore, it is necessary to apply other techniques, and we
shall rely on second quantization, quantum field theory, and the
use of GREEN's functions.
-body wave function
contains all information, but a direct solution of the SCHRÖDINGER equation
is impractical. Therefore, it is necessary to apply other techniques, and we
shall rely on second quantization, quantum field theory, and the
use of GREEN's functions.
Historically, quantum physics first dealt only with the quantization of the
motion of particles, leaving the electromagnetic field classical (SCHRÖDINGER,
HEISENBERG, and DIRAC, 1925-26). Later also the electromagnetic field was
quantized (DIRAC, 1927), and even the particles themselves got represented by
quantized fields (JORDAN and WIGNER, 1927), resulting in the development of
quantum electrodynamics and quantum field theory in general.
By convention, the
original form of quantum mechanics is denoted first quantization, while quantum
field theory is formulated in the language of second quantization. Second
quantization greatly simplifies the discussion of many interacting
particles. This approach merely reformulates the original
SCHRÖDINGER equation. Nevertheless, it has the advantage that in second quantization
operators incorporate the statistics, which contrasts with the
more cumbersome approach of using symmetrized or anti-symmetrized products of
single-particle wave functions.
In the second quantization formalism a quantum mechanical basis is used that
describes the number of particles occupying each state in a complete set of
single-particle states. For this purpose the time-independent abstract state vectors
for an  -particle system are introduced
-particle system are introduced
 |
(A.3) |
The notation means that there are 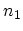 particles in the state
particles in the state
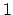 ,
, 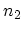 particles in the state
particles in the state 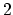 , and so forth. It is
therefore natural to define occupation number operators
, and so forth. It is
therefore natural to define occupation number operators
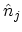 which have the basis states
which have the basis states
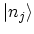 as eigenstates, and have the
number
as eigenstates, and have the
number 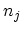 of particles occupying the state
of particles occupying the state 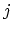 as eigenvalues
as eigenvalues
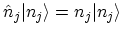 . For
FERMIons
. For
FERMIons 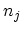 can be 0 or
can be 0 or 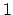 , while for Bosons it can be any
non-negative number.
, while for Bosons it can be any
non-negative number.
To connect first and second quantization, annihilation and creation operators 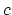 and
and
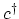 for FERMIons and
for FERMIons and 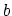 and
and 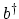 for Bosons are introduced.
These operators satisfy either the commutationA.1 or anti-commutationA.2 rules
for Bosons are introduced.
These operators satisfy either the commutationA.1 or anti-commutationA.2 rules
![\begin{displaymath}\begin{array}{ll} [c_{i},c_{j}]_{+} \ = \ 0\ , \hspace*{40pt}...
...{40pt} [b_{i}^\dagger,b_{j}^\dagger]_{-} \ = \ 0\ . \end{array}\end{displaymath}](img1066.png) |
(A.4) |
All of the properties
of these operators follow directly from the commutation or anti-commutation
rules. The annihilation operators, 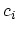 and
and 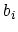 , decrease the
occupation number of the state
, decrease the
occupation number of the state 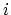 by 1, whereas the creation operators,
by 1, whereas the creation operators,
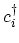 and
and
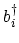 , increase the occupation number
of the state
, increase the occupation number
of the state 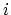 by 1.
by 1.
The HAMILTONian in (A.1) can be written in terms of
annihilation and creation operators
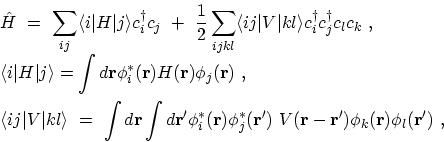 |
(A.5) |
where
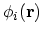 are the single-particle wave functions and
the circumflex denotes an operator in the abstract occupation-number
Hilbert space. In this form, the matrix elements of the single-particle HAMILTONian
and the interaction potential taken between the single-particle
eigenstates of the SCHRÖDINGER equation in first quantization are merely complex
numbers multiplying operators.
are the single-particle wave functions and
the circumflex denotes an operator in the abstract occupation-number
Hilbert space. In this form, the matrix elements of the single-particle HAMILTONian
and the interaction potential taken between the single-particle
eigenstates of the SCHRÖDINGER equation in first quantization are merely complex
numbers multiplying operators.
It is often convenient to form a linear
combination of the annihilation and creation operators
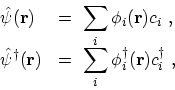 |
(A.6) |
where the sum is over the complete set of single-particle quantum numbers. The
so-called field operators
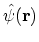 and
and
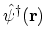 satisfy
simple commutation or anti-commutation relations
satisfy
simple commutation or anti-commutation relations
![\begin{displaymath}\begin{array}{lll} \displaystyle [\hat{\psi}({\bf {r}}),\hat{...
...,\hat{\psi}^\dagger({\bf {r'}})]_{\pm} \ & = \ 0\ , \end{array}\end{displaymath}](img1076.png) |
(A.7) |
where the plus (minus) sign refers to FERMIons (Bosons).
The field operator
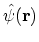 annihilates and
annihilates and
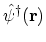 creates a particle at place
creates a particle at place 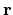 . The HAMILTONian operator can be rewritten in
terms of these field operators as follows
. The HAMILTONian operator can be rewritten in
terms of these field operators as follows
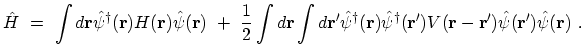 |
(A.8) |
In this form, the HAMILTONian suggests the name second quantization,
since the above expression looks like the expectation value of the HAMILTON
ian taken between wave functions. Both (A.5)
and (A.8) are equivalent since the integration over spatial
coordinates produces the single-particle matrix elements of the kinetic energy,
potential and interaction potential energy, leaving a sum of these
matrix elements multiplied by the appropriate annihilation and creation
operators.
The methods of quantum field theory also allow us to concentrate on the few
matrix elements of interest, thus avoiding the need for dealing directly with
the many-particle wave function and the coordinates of all the remaining
particles. Finally, the GREEN's functions contain the most important physical
information such as the ground-state energy and other thermodynamic functions,
the energy and life time of excited states, and the response to external
perturbations. Unfortunately, the exact GREEN's functions are not easier to
determine than the original wave function, and we therefore make use of
perturbation theory which can be expressed in the systematic language of
FEYNMAN rules and diagrams. These rules allow one to evaluate physical
quantities to any perturbation order.
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() -particle system are introduced
-particle system are introduced

![]() and
and
![]() for FERMIons and
for FERMIons and ![]() and
and ![]() for Bosons are introduced.
These operators satisfy either the commutationA.1 or anti-commutationA.2 rules
for Bosons are introduced.
These operators satisfy either the commutationA.1 or anti-commutationA.2 rules