B.5 Imaginary Time Operators

At finite temperature under thermodynamic equilibrium the state of a system is described by the equilibrium density operator 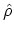$\hat{\rho}$ . For a given 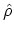$\hat{\rho}$ the ensemble average of any operator 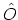$\hat{O}$ can be calculated as (see (3.11))

$\begin{displaymath}\begin{array}{ll}\displaystyle \langle \hat{O}\rangle \ &\dis... ...{K}} \hat{O}]} {\mathrm{Tr}[e^{-\beta\hat{K}}]} \ , \end{array}\end{displaymath}$

(B.25)

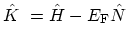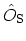where $\hat{K}\ = \hat{H}-E_\mathrm{F}\hat{N}$ may be interpreted as a grand canonical HAMILTONian. For any SCHRÖDINGER operator $\hat{O}_\mathrm{S}$ , the so called modified HEISENBERG and interaction pictures can be introduced as

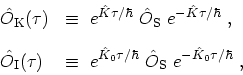$\begin{displaymath}\begin{array}{ll}\displaystyle \hat{O}_\mathrm{K}(\tau)&\disp... ... \ \hat{O}_\mathrm{S}\ e^{-\hat{K}_0\tau/\hbar} \ , \end{array}\end{displaymath}$

(B.26)

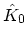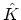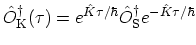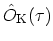where $\hat{K}_0$ includes only the non-interacting part of $\hat{K}$ . It should be noticed that $\hat{O}_\mathrm{K}^\dagger(\tau)= e^{\hat{K}\tau/\hbar}\hat{O}_\mathrm{S}^\dagger e^{-\hat{K}\tau/\hbar}$ is not the adjoint of $\hat{O}_\mathrm{K}(\tau)$ as long as 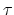$\tau$ is real. If 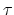$\tau$ is interpreted as a complex variable, however, it may be analytically continued to a pure imaginary value 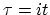$\tau=it$ . 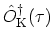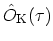The resulting expression $\hat{O}^\dagger_\mathrm{K}(\tau)$ then becomes the true adjoint of $\hat{O}_\mathrm{K}(\tau)$ and is formally identical with the original HEISENBERG picture defined in (B.12), apart from the substitution of $\hat{K}$ for $\hat{H}$ . 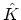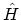For this reason (B.26) are sometimes called imaginary-time operators.

The modified HEISENBERG and interaction pictures are related by (compare (B.13) and (B.14))

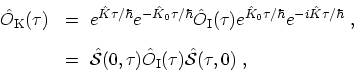$\begin{displaymath}\begin{array}{ll} \displaystyle \hat{O}_\mathrm{K}(\tau) \ & ... ...at{O}_\mathrm{I}(\tau) \mathcal{\hat{S}}(\tau,0) \ ,\end{array}\end{displaymath}$

(B.27)

where the operator 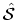$\mathcal{\hat{S}}$ is defined by (compare (B.17))

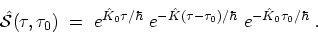$\begin{displaymath}\begin{array}{l}\displaystyle \mathcal{\hat{S}}(\tau,\tau_0) ... ...tau-\tau_0)/\hbar} \ e^{-\hat{K}_0\tau_0/\hbar} \ . \end{array}\end{displaymath}$

(B.28)

Note that 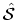$\mathcal{\hat{S}}$ is not unitary, but it still satisfies the group property

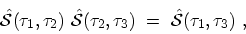$\begin{displaymath}\begin{array}{l}\displaystyle \mathcal{\hat{S}}(\tau_1,\tau_2... ...,\tau_3) \ = \ \mathcal{\hat{S}}(\tau_1,\tau_3) \ , \end{array}\end{displaymath}$

(B.29)

and the boundary condition

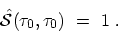$\begin{displaymath}\begin{array}{l}\displaystyle \mathcal{\hat{S}}(\tau_0,\tau_0) \ = \ 1 \ . \end{array}\end{displaymath}$

(B.30)

In addition, the equation of motion of 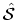$\mathcal{\hat{S}}$ is calculated as

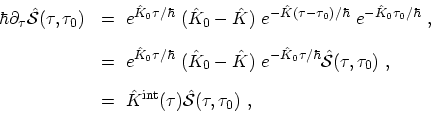$\begin{displaymath}\begin{array}{ll}\displaystyle \hbar \partial_\tau \mathcal{\... ...athrm{int}(\tau) \mathcal{\hat{S}}(\tau,\tau_0) \ , \end{array}\end{displaymath}$

(B.31)

where

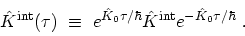$\begin{displaymath}\begin{array}{l}\displaystyle \hat{K}^\mathrm{int}(\tau) \ \e... ...r}\hat{K}^\mathrm{int} e^{-\hat{K}_0\tau/\hbar} \ . \end{array}\end{displaymath}$

(B.32)

It follows that the operator 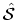$\mathcal{\hat{S}}$ obeys essentially the same differential equation as the unitary operator introduced in (B.15), and one may immediately write down the solution (compare (B.24))

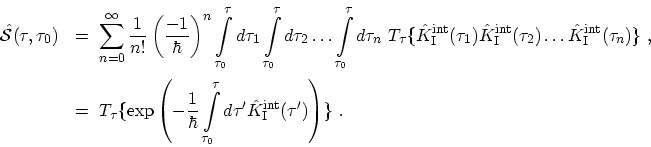$\begin{displaymath}\begin{array}{ll} \displaystyle \mathcal{\hat{S}}(\tau,\tau_0... ...at{K}^\mathrm{int}_\mathrm{I}(\tau') \right) \} \ . \end{array}\end{displaymath}$

(B.33)

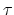If $\tau$ is set equal to 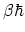$\beta\hbar$ , (B.28) may be rewritten as

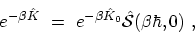$\begin{displaymath}\begin{array}{l}\displaystyle e^{-\beta\hat{K}} \ = \ e^{-\beta\hat{K}_0} \mathcal{\hat{S}}(\beta\hbar,0) \ , \end{array}\end{displaymath}$

(B.34)

which relates the many particle density operator to the single-particle density operator by means of an imaginary time-evolution operator. M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors


Previous: B.4 The Evolution Operator Up: B. Time Evolution Pictures Next: C. Review of Thermodynamics and Statistical Mechanics