C. Review of Thermodynamics and Statistical Mechanics
The fundamental thermodynamic identity
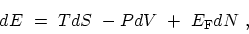 |
(C.1) |
specifies the change in the internal energy 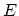 arising from small independent
changes in the entropy
arising from small independent
changes in the entropy 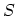 , the volume
, the volume 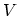 , and the number of particles
, and the number of particles 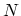 .
Equation (C.1) shows that the internal energy is a function of these
three variables,
.
Equation (C.1) shows that the internal energy is a function of these
three variables,
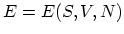 , and that the temperature
, and that the temperature 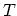 , the pressure
, the pressure 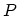 ,
and the FERMI energy
,
and the FERMI energy
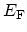 (also called the chemical potential) are related to
the partial derivatives of
(also called the chemical potential) are related to
the partial derivatives of 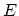
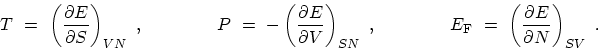 |
(C.2) |
In practice, however, experiments are usually performed at fixed 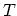 and it is
convenient to make LEGENDRE transformation to the variables
and it is
convenient to make LEGENDRE transformation to the variables 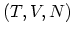 or
or
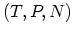 . The resulting functions are known as HELMHOLTZ free energy
. The resulting functions are known as HELMHOLTZ free energy
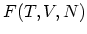 and GIBBS free energy
and GIBBS free energy 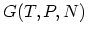 . It is often important to
consider the set of independent variables
. It is often important to
consider the set of independent variables
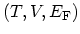 , which is appropriate for
variable
, which is appropriate for
variable 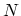 . A further LEGENDRE transformation leads to the
thermodynamic potential
. A further LEGENDRE transformation leads to the
thermodynamic potential
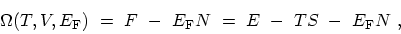 |
(C.3) |
with the corresponding differential and coefficients
 |
(C.4) |
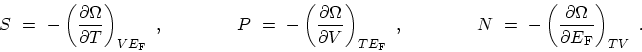 |
(C.5) |
Although 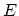 ,
, 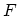 ,
, 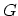 , and
, and 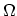 represent equivalent ways of describing
the same system, their natural independent variables differ in one important
way. In particular, the set
represent equivalent ways of describing
the same system, their natural independent variables differ in one important
way. In particular, the set 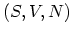 consists entirely of extensive
variables, proportional to the actual amount of matter present. The
transformation to
consists entirely of extensive
variables, proportional to the actual amount of matter present. The
transformation to 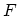 and then to
and then to 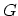 or
or 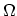 may be interpreted as
reducing the number of extensive variables in favor of intensive ones that are
independent of the total amount of matter.
may be interpreted as
reducing the number of extensive variables in favor of intensive ones that are
independent of the total amount of matter.
To this point, only macroscopic thermodynamics has been discussed. The
microscopic content of the theory must be added separately through statistical
mechanics, which relates the thermodynamic functions to the HAMILTONian of
the many-particle system. The elementary discussions of statistical mechanics
usually consider systems containing a fixed number of particles. This approach,
which is refereed to as canonical ensemble, is too restricted for our
purposes. To include the possibility of a variable number of particles the
grand canonical ensemble can be employed. For a grand canonical
ensemble at FERMI energy
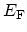 and temperature
and temperature 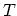 , the grand partition
function
, the grand partition
function 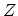 is defined as
is defined as
![\begin{displaymath}\begin{array}{ll} Z\ &\displaystyle \equiv \ \sum_{N} \sum_{i...
...{Tr}[e^{-\beta(\hat{H}- E_\mathrm{F} \hat{N})}] \ , \end{array}\end{displaymath}](img1148.png) |
(C.6) |
where 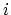 denotes the set of all states for a fixed number of particles
denotes the set of all states for a fixed number of particles 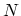 , and
the sum implied in the trace is over both
, and
the sum implied in the trace is over both 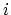 and
and 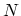 . Short-hand notation
. Short-hand notation
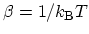 has been introduced, where
has been introduced, where
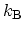 is the
BOLTZMANN constant. A fundamental result from statistical mechanics states
that
is the
BOLTZMANN constant. A fundamental result from statistical mechanics states
that
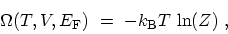 |
(C.7) |
which allows one to compute all the macroscopic equilibrium thermodynamics from
the grand partition function. The statistical operator 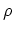 corresponding
to (C.6) is given by
corresponding
to (C.6) is given by
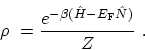 |
(C.8) |
For any operator 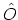 , the ensemble average
, the ensemble average
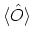 is
achieved with the prescription
is
achieved with the prescription
![\begin{displaymath}\begin{array}{ll}\displaystyle \langle \hat{O}\rangle \ &\dis...
...Tr}[e^{-\beta(\hat{H}- E_\mathrm{F} \hat{N})}]} \ . \end{array}\end{displaymath}](img1153.png) |
(C.9) |
By applying these results the properties of a gas of non-interacting Bosons or
FERMIons can be studied. If (C.6) is written out in detail
with the complete set of states in the abstract occupation number
HILBERT space, one gets
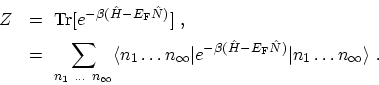 |
(C.10) |
Since these states are eigen-states of the non-interacting
HAMILTONian
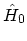 and the number operator
and the number operator 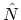 , both
operators can be replaced by their eigen-values
, both
operators can be replaced by their eigen-values
![\begin{displaymath}\begin{array}{ll}\displaystyle Z\ &\displaystyle = \ \sum_{n_...
...\right)\right] \vert n_1\ldots n_\infty \rangle \ . \end{array}\end{displaymath}](img1155.png) |
(C.11) |
The exponential is now a number and is equivalent to a product of
exponentials. Therefore, the sum over expectation values factor into a product
of traces
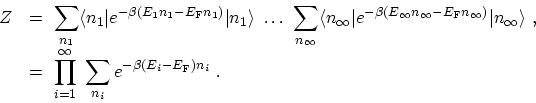 |
(C.12) |
Subsections
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() and temperature
and temperature ![]() , the grand partition
function
, the grand partition
function ![]() is defined as
is defined as
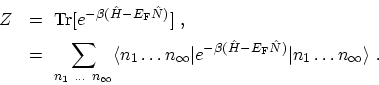
![\begin{displaymath}\begin{array}{ll}\displaystyle Z\ &\displaystyle = \ \sum_{n_...
...\right)\right] \vert n_1\ldots n_\infty \rangle \ . \end{array}\end{displaymath}](img1155.png)