F.2 Electron-Phonon Interaction
The coupling of electrons and nuclei in the lattice to the external sources is given by
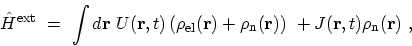 |
(F.24) |
where
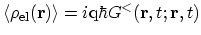 is the
density of electrons. The density of the nuclei in the lattice
is the
density of electrons. The density of the nuclei in the lattice
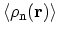 is represented as a sum of local
charge densities
is represented as a sum of local
charge densities
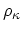
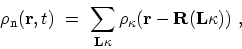 |
(F.25) |
where the actual positions of the nuclei
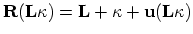 , is defined in terms of the equilibrium lattice vector
, is defined in terms of the equilibrium lattice vector 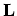 , the basis vector within the unit cell
, the basis vector within the unit cell
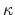 , and the lattice
displacement
, and the lattice
displacement
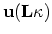 . In case of bare nuclei,
. In case of bare nuclei,
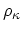 would approximately be
would approximately be 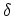 functions. However, it is more convenient to
consider rigid ion cores instead of bare nuclei. In this case
functions. However, it is more convenient to
consider rigid ion cores instead of bare nuclei. In this case
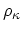 denotes the charge density of the ion cores.
denotes the charge density of the ion cores.
For a simple derivation of the electron-phonon interaction, one has to add an
additional external source
 in (F.24) [203], which couples to the charge density of
the nuclei and is merely a mathematical trick, see (F.32)-(F.35).
With similar steps for deriving (F.7), one can show that under the HAMILTONian
in (F.24) the effective potential can be written as
in (F.24) [203], which couples to the charge density of
the nuclei and is merely a mathematical trick, see (F.32)-(F.35).
With similar steps for deriving (F.7), one can show that under the HAMILTONian
in (F.24) the effective potential can be written as
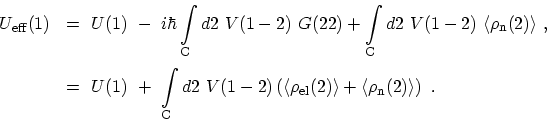 |
(F.26) |
The aim is the calculation of the total linear response of the system,
including the contribution from the nuclei, i.e. the variation of the total
electrostatic potential with the external potential [205]
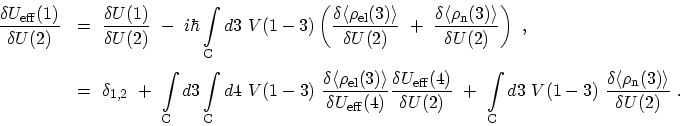 |
(F.27) |
Solving with respect to
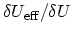 , one obtains
, one obtains
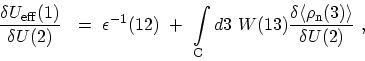 |
(F.28) |
where the dielectric function is
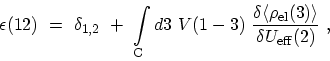 |
(F.29) |
and 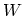 is the screened interaction. The derivative
is the screened interaction. The derivative
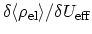 differs from the
purely electronic polarization which is introduced in Appendix F.1.1, owing to
the phonon contribution to the total potential. Neglecting this phonon
contribution to the polarization function is one of the ingredients of the adiabatic approximation [246]. This approximation reduces the
dielectric function and the screened interaction in (F.28) to
the purely electronic quantities which are introduced
in (F.20) and (F.21). The next step is the
calculation of the lattice contribution. Similar to the GREEN's
function for electrons, one can consider the expectation value of the density
of nuclei
differs from the
purely electronic polarization which is introduced in Appendix F.1.1, owing to
the phonon contribution to the total potential. Neglecting this phonon
contribution to the polarization function is one of the ingredients of the adiabatic approximation [246]. This approximation reduces the
dielectric function and the screened interaction in (F.28) to
the purely electronic quantities which are introduced
in (F.20) and (F.21). The next step is the
calculation of the lattice contribution. Similar to the GREEN's
function for electrons, one can consider the expectation value of the density
of nuclei
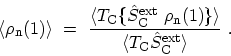 |
(F.30) |
With similar steps for deriving (F.5), the density
response of the nuclei under the action of
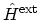 can be
calculated as
can be
calculated as
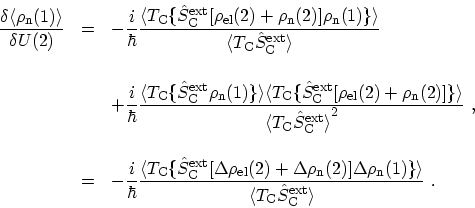 |
(F.31) |
In the last step, the deviation operator
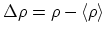 is introduced. Furthermore, the relation
is introduced. Furthermore, the relation
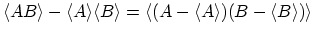 is used. Now the additional external field
is used. Now the additional external field 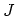 comes into play, which
allows us to eliminate the mixed electron-nuclei contribution. By steps
completely analogous to those used before, one finds
comes into play, which
allows us to eliminate the mixed electron-nuclei contribution. By steps
completely analogous to those used before, one finds
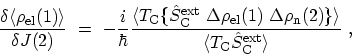 |
(F.32) |
which together with (F.31), yields the result
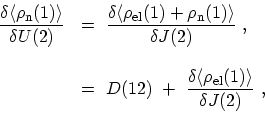 |
(F.33) |
where the density-density correlation function of the nuclei is defined as
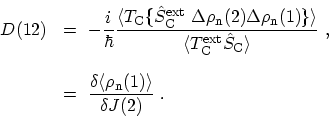 |
(F.34) |
One can again apply the chain rule to (F.33) to eliminate the
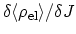 contribution.
contribution.
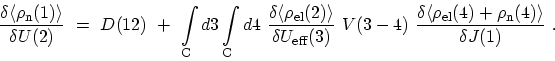 |
(F.35) |
Making use of the relation (F.33) once more, one can solve the
resulting equation with respect to
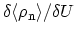 and express the solution in terms of the
dielectric function. After insertion in (F.28), this
yields the total dielectric screening function as
and express the solution in terms of the
dielectric function. After insertion in (F.28), this
yields the total dielectric screening function as
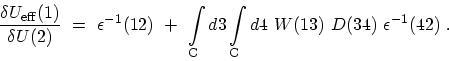 |
(F.36) |
The desired effective electron-electron interaction induced by lattice
vibrations is thus finally given by [205]
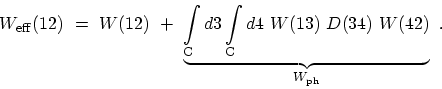 |
(F.37) |
Therefore, the problem of electron-phonon interaction is reduced to the
replacement of the electronically screened interaction introduced
in Appendix F.1.1 by the effective interaction (F.37).
Subsections
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() in (F.24) [203], which couples to the charge density of
the nuclei and is merely a mathematical trick, see (F.32)-(F.35).
With similar steps for deriving (F.7), one can show that under the HAMILTONian
in (F.24) the effective potential can be written as
in (F.24) [203], which couples to the charge density of
the nuclei and is merely a mathematical trick, see (F.32)-(F.35).
With similar steps for deriving (F.7), one can show that under the HAMILTONian
in (F.24) the effective potential can be written as