The structure of CNTs has been explored early by high resolution
transmission electron microscopy techniques yielding direct confirmation that
the CNTs are seamless cylinders derived from the honeycomb lattice representing
a single atomic layer of crystalline graphite, called a graphene sheet.
The structure of a SW-CNT is conveniently explained in
terms of its one-dimensional unit cell, defined by the vectors 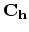 and
and
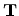 as shown in Fig. 2.2.
as shown in Fig. 2.2.
The circumference of any CNT is expressed in terms of the chiral vector
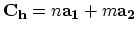 which connects two crystallographically equivalent
sites on a two-dimensional graphene sheet [16]. The construction
in Fig. 2.2 depends uniquely on the pair of integers
which connects two crystallographically equivalent
sites on a two-dimensional graphene sheet [16]. The construction
in Fig. 2.2 depends uniquely on the pair of integers 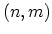 which
specify the chiral vector. The chiral angle
which
specify the chiral vector. The chiral angle 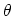 is defined as the angle
between the chiral vector
is defined as the angle
between the chiral vector  and the zigzag direction
(
and the zigzag direction
(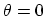 ). Three distinct types of CNT structures
can be generated by rolling up the graphene sheet into a cylinder as
shown in Fig. 2.3. The zigzag and armchair
CNTs correspond to chiral angles of
). Three distinct types of CNT structures
can be generated by rolling up the graphene sheet into a cylinder as
shown in Fig. 2.3. The zigzag and armchair
CNTs correspond to chiral angles of 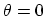 and
and
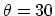 °, respectively, and chiral CNTs correspond to
°, respectively, and chiral CNTs correspond to
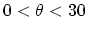 °. The intersection of the vector
°. The intersection of the vector
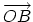 (which is normal to
(which is normal to 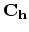 ) with the first lattice
point determines the fundamental one-dimensional translation vector
) with the first lattice
point determines the fundamental one-dimensional translation vector 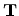 . The unit cell of the one-dimensional lattice is the rectangle defined by
the vectors
. The unit cell of the one-dimensional lattice is the rectangle defined by
the vectors 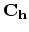 and
and 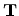 .
.
The cylinder connecting the two hemispherical caps of the CNT
(see Fig. 2.3) is formed by superimposing the two ends of the vector
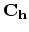 and the cylinder joint is made along the two lines
and the cylinder joint is made along the two lines
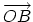 and
and
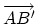 in Fig. 2.2. The lines
in Fig. 2.2. The lines
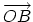 and
and
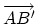 are both perpendicular to the
vector
are both perpendicular to the
vector 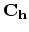 at each end of
at each end of 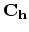 [16]. In the
[16]. In the
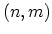 notation for
notation for
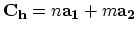 , the vectors
, the vectors 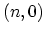 or
or
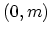 denote zigzag CNTs, whereas the vectors
denote zigzag CNTs, whereas the vectors 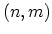 correspond to chiral
CNTs [21]. The CNT diameter
correspond to chiral
CNTs [21]. The CNT diameter
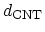 is given by
is given by
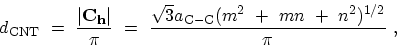 |
(2.1) |
where
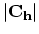 is the length of
is the length of 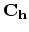 and
and
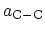 is the C-C
bond length (1.42 Å). The chiral angle
is the C-C
bond length (1.42 Å). The chiral angle 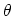 is given by
is given by
![$ \theta \ = \
\mathrm{tan}^{-1}[\sqrt{3}n/(2m\ + \ n)]$](img202.png) . For the
. For the 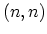 armchair CNT
armchair CNT
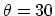 ° and for the
° and for the 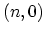 zigzag CNT
zigzag CNT 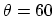 °.
From Fig. 2.2 it follows
that if one limits
°.
From Fig. 2.2 it follows
that if one limits 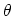 to the range
to the range
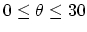 °, then
by symmetry,
°, then
by symmetry, 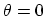 for a zigzag CNT. Both armchair and zigzag CNTs have a
mirror plane and thus are considered achiral. Differences in the CNT
diameter
for a zigzag CNT. Both armchair and zigzag CNTs have a
mirror plane and thus are considered achiral. Differences in the CNT
diameter
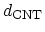 and chiral angle
and chiral angle 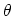 give rise to different
properties of the various CNTs. The number
give rise to different
properties of the various CNTs. The number 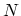 of hexagons per unit cell of
a CNT, specified by integers
of hexagons per unit cell of
a CNT, specified by integers 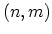 , is given by
, is given by
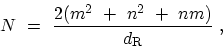 |
(2.2) |
where
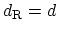 if
if 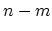 is not a multiple of
is not a multiple of 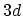 , and
, and
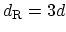 if
if 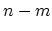 is a multiple of
is a multiple of 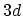 , and
, and 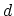 is defined as the greatest common divisor
(gcd) of
is defined as the greatest common divisor
(gcd) of 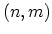 . Each hexagon in the honeycomb lattice contains two carbon atoms.
The unit cell area of the CNT is
. Each hexagon in the honeycomb lattice contains two carbon atoms.
The unit cell area of the CNT is 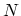 times larger
than that for a graphene layer and consequently the unit cell area for the CNT
in reciprocal space is correspondingly
times larger
than that for a graphene layer and consequently the unit cell area for the CNT
in reciprocal space is correspondingly 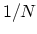 times smaller. Table 2.2
provides a summary of relations useful for describing the structure of
SW-CNTs [12,22].
times smaller. Table 2.2
provides a summary of relations useful for describing the structure of
SW-CNTs [12,22].
Figure 2.2:
The chiral vector
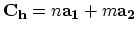 is defined on the honeycomb lattice of carbon atoms by unit
vectors
is defined on the honeycomb lattice of carbon atoms by unit
vectors 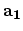 and
and 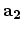 and the chiral angle
and the chiral angle 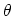 with
respect to the zigzag axis (
with
respect to the zigzag axis (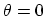 ). The diagram is constructed for
). The diagram is constructed for
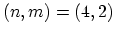 .
.
|
|
Figure 2.3:
Schematic models of SW-CNTs with the CNT axis
normal to the chiral vector. The latter is along (a) the
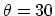 ° direction for an
° direction for an 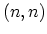 armchair CNT, (b) the
armchair CNT, (b) the
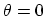 direction for a
direction for a 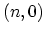 zigzag CNT, and (c) a general
zigzag CNT, and (c) a general 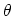 direction with
direction with
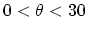 ° for a
° for a 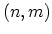 chiral CNT.
chiral CNT.
|
|
Table 2.2:
Structural properties for CNTs [12].
| |
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() which connects two crystallographically equivalent
sites on a two-dimensional graphene sheet [16]. The construction
in Fig. 2.2 depends uniquely on the pair of integers
which connects two crystallographically equivalent
sites on a two-dimensional graphene sheet [16]. The construction
in Fig. 2.2 depends uniquely on the pair of integers ![]() which
specify the chiral vector. The chiral angle
which
specify the chiral vector. The chiral angle ![]() is defined as the angle
between the chiral vector
is defined as the angle
between the chiral vector ![]() and the zigzag direction
(
and the zigzag direction
(![]() ). Three distinct types of CNT structures
can be generated by rolling up the graphene sheet into a cylinder as
shown in Fig. 2.3. The zigzag and armchair
CNTs correspond to chiral angles of
). Three distinct types of CNT structures
can be generated by rolling up the graphene sheet into a cylinder as
shown in Fig. 2.3. The zigzag and armchair
CNTs correspond to chiral angles of ![]() and
and
![]() °, respectively, and chiral CNTs correspond to
°, respectively, and chiral CNTs correspond to
![]() °. The intersection of the vector
°. The intersection of the vector
![]() (which is normal to
(which is normal to ![]() ) with the first lattice
point determines the fundamental one-dimensional translation vector
) with the first lattice
point determines the fundamental one-dimensional translation vector ![]() . The unit cell of the one-dimensional lattice is the rectangle defined by
the vectors
. The unit cell of the one-dimensional lattice is the rectangle defined by
the vectors ![]() and
and ![]() .
.
![]() and the cylinder joint is made along the two lines
and the cylinder joint is made along the two lines
![]() and
and
![]() in Fig. 2.2. The lines
in Fig. 2.2. The lines
![]() and
and
![]() are both perpendicular to the
vector
are both perpendicular to the
vector ![]() at each end of
at each end of ![]() [16]. In the
[16]. In the
![]() notation for
notation for
![]() , the vectors
, the vectors ![]() or
or
![]() denote zigzag CNTs, whereas the vectors
denote zigzag CNTs, whereas the vectors ![]() correspond to chiral
CNTs [21]. The CNT diameter
correspond to chiral
CNTs [21]. The CNT diameter
![]() is given by
is given by
![\includegraphics[width=.5\textwidth]{figures/2D-CNT.eps}](img212.png)
![\includegraphics[width=.5\textwidth]{figures/CNT_Types.eps}](img213.png)