2. Fundamentals of Carbon Nanotubes
CARBON MATERIALS are found in a variety of forms such as fullerenes, graphite,
carbon fibres, carbon nanotubes, and diamond. The reason why carbon assumes
many structural forms is that a carbon atom can form several distinct types of
orbital hybridization. The 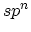 hybridization is essential for determining
the dimensionality of not only carbon based molecules but also carbon based
solids. Carbon is the only element in the periodic table that has isomers from
zero-dimensions to three-dimensions, see Table 2. In
hybridization is essential for determining
the dimensionality of not only carbon based molecules but also carbon based
solids. Carbon is the only element in the periodic table that has isomers from
zero-dimensions to three-dimensions, see Table 2. In 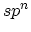 hybridization,
hybridization, 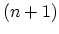
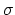 bonds per carbon atom are formed, which
form a skeleton for the local structure of the
bonds per carbon atom are formed, which
form a skeleton for the local structure of the 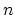 -dimensional
structure. In
-dimensional
structure. In 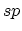 hybridization, two
hybridization, two 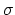 bonds form a
one-dimensional chain structure, which is known as a carbyne. Interestingly,
bonds form a
one-dimensional chain structure, which is known as a carbyne. Interestingly,
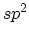 hybridization, which forms a planer structure in two-dimensional
graphite, also forms a planar local structure in the closed polyhedra of the (zero-dimensional)
fullerene family and the one-dimensional cylinders called carbon
nanotubes (CNTs). Carbon fibers which are macroscopic one-dimensional
materials are closely related to CNTs, because of their characteristic high
length to diameter ratio. A carbon fiber, however, consists of many graphite
planes and microscopically exhibits electronic properties that are
predominantly two-dimensional. Amorphous graphite, showing mainly
hybridization, which forms a planer structure in two-dimensional
graphite, also forms a planar local structure in the closed polyhedra of the (zero-dimensional)
fullerene family and the one-dimensional cylinders called carbon
nanotubes (CNTs). Carbon fibers which are macroscopic one-dimensional
materials are closely related to CNTs, because of their characteristic high
length to diameter ratio. A carbon fiber, however, consists of many graphite
planes and microscopically exhibits electronic properties that are
predominantly two-dimensional. Amorphous graphite, showing mainly
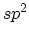 hybridization, consisting of randomly stacked graphite layer
segments. Because of the weak inter-planer interaction between two graphite
planes, they can move easily relative to each other, thereby forming
a solid lubricant. In this sense, amorphous graphite can behave like a
two-dimensional material. Four
hybridization, consisting of randomly stacked graphite layer
segments. Because of the weak inter-planer interaction between two graphite
planes, they can move easily relative to each other, thereby forming
a solid lubricant. In this sense, amorphous graphite can behave like a
two-dimensional material. Four 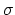 bonds defining a regular tetrahedron
are sufficient to form a three-dimensional structure known as the diamond
structure. Amorphous carbon is a disordered, three-dimensional material in
which both
bonds defining a regular tetrahedron
are sufficient to form a three-dimensional structure known as the diamond
structure. Amorphous carbon is a disordered, three-dimensional material in
which both 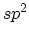 and
and 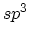 hybridization is present.
hybridization is present.
CNTs are unique nano-structures that can be considered conceptually a
prototype one-dimensional quantum wire. The fundamental building block of CNTs
is the very long, all-carbon cylindrical single-wall CNT (SW-CNT), one atom in
wall thickness and tens of atoms around the circumference (typical diameter
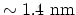 ). Initially, CNTs gained great interest in research
community because of their exotic electronic properties, and this interest
continued as other remarkable properties were discovered and promise of
practical applications developed. In this chapter, a brief historical review of
CNT research is presented and some basic definitions relevant to the structural
properties of CNTs are provided. Finally, application of CNTs in electronics, especially
CNT based transistors, are discussed.
). Initially, CNTs gained great interest in research
community because of their exotic electronic properties, and this interest
continued as other remarkable properties were discovered and promise of
practical applications developed. In this chapter, a brief historical review of
CNT research is presented and some basic definitions relevant to the structural
properties of CNTs are provided. Finally, application of CNTs in electronics, especially
CNT based transistors, are discussed.
Table 2.1:
Important carbon isomers [12].
| Dimension |
0-D |
1-D |
2-D |
3-D |
| Isomer |
Fullerene |
Nanotubes |
Graphite |
Diamond |
| Hybridization |
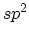 |
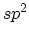 |
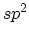 |
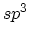 |
Density
![$ \mathrm{[g/cm^3]}$](img181.png) |
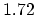 |
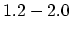 |
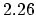 |
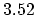 |
| Bond
Length (Å) |
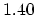 (C=C) (C=C) |
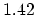 (C=C) (C=C) |
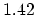 (C=C) (C=C) |
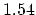 (C-C) (C-C) |
| Electronic Properties |
Semiconductor
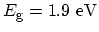 |
Semiconductor or Metal |
Semi-metal |
Insulator
 |
|
Subsections
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() hybridization is essential for determining
the dimensionality of not only carbon based molecules but also carbon based
solids. Carbon is the only element in the periodic table that has isomers from
zero-dimensions to three-dimensions, see Table 2. In
hybridization is essential for determining
the dimensionality of not only carbon based molecules but also carbon based
solids. Carbon is the only element in the periodic table that has isomers from
zero-dimensions to three-dimensions, see Table 2. In ![]() hybridization,
hybridization, ![]()
![]() bonds per carbon atom are formed, which
form a skeleton for the local structure of the
bonds per carbon atom are formed, which
form a skeleton for the local structure of the ![]() -dimensional
structure. In
-dimensional
structure. In ![]() hybridization, two
hybridization, two ![]() bonds form a
one-dimensional chain structure, which is known as a carbyne. Interestingly,
bonds form a
one-dimensional chain structure, which is known as a carbyne. Interestingly,
![]() hybridization, which forms a planer structure in two-dimensional
graphite, also forms a planar local structure in the closed polyhedra of the (zero-dimensional)
fullerene family and the one-dimensional cylinders called carbon
nanotubes (CNTs). Carbon fibers which are macroscopic one-dimensional
materials are closely related to CNTs, because of their characteristic high
length to diameter ratio. A carbon fiber, however, consists of many graphite
planes and microscopically exhibits electronic properties that are
predominantly two-dimensional. Amorphous graphite, showing mainly
hybridization, which forms a planer structure in two-dimensional
graphite, also forms a planar local structure in the closed polyhedra of the (zero-dimensional)
fullerene family and the one-dimensional cylinders called carbon
nanotubes (CNTs). Carbon fibers which are macroscopic one-dimensional
materials are closely related to CNTs, because of their characteristic high
length to diameter ratio. A carbon fiber, however, consists of many graphite
planes and microscopically exhibits electronic properties that are
predominantly two-dimensional. Amorphous graphite, showing mainly
![]() hybridization, consisting of randomly stacked graphite layer
segments. Because of the weak inter-planer interaction between two graphite
planes, they can move easily relative to each other, thereby forming
a solid lubricant. In this sense, amorphous graphite can behave like a
two-dimensional material. Four
hybridization, consisting of randomly stacked graphite layer
segments. Because of the weak inter-planer interaction between two graphite
planes, they can move easily relative to each other, thereby forming
a solid lubricant. In this sense, amorphous graphite can behave like a
two-dimensional material. Four ![]() bonds defining a regular tetrahedron
are sufficient to form a three-dimensional structure known as the diamond
structure. Amorphous carbon is a disordered, three-dimensional material in
which both
bonds defining a regular tetrahedron
are sufficient to form a three-dimensional structure known as the diamond
structure. Amorphous carbon is a disordered, three-dimensional material in
which both ![]() and
and ![]() hybridization is present.
hybridization is present.
![]() ). Initially, CNTs gained great interest in research
community because of their exotic electronic properties, and this interest
continued as other remarkable properties were discovered and promise of
practical applications developed. In this chapter, a brief historical review of
CNT research is presented and some basic definitions relevant to the structural
properties of CNTs are provided. Finally, application of CNTs in electronics, especially
CNT based transistors, are discussed.
). Initially, CNTs gained great interest in research
community because of their exotic electronic properties, and this interest
continued as other remarkable properties were discovered and promise of
practical applications developed. In this chapter, a brief historical review of
CNT research is presented and some basic definitions relevant to the structural
properties of CNTs are provided. Finally, application of CNTs in electronics, especially
CNT based transistors, are discussed.