3.3.2 Contour-Ordered GREEN's Function
To express the field operators in the interaction representation an
operator 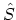 is defined (see Appendix B.4) and applied
for calculating the GREEN's functions as in Section 3.1.1. The time
in (3.8) is taken over the interval
is defined (see Appendix B.4) and applied
for calculating the GREEN's functions as in Section 3.1.1. The time
in (3.8) is taken over the interval
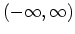 . The
state at
. The
state at
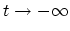 is well defined as the ground-state of the
non-interacting system
is well defined as the ground-state of the
non-interacting system
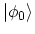 . The interactions are turned on
slowly. At
. The interactions are turned on
slowly. At 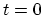 the fully interacting ground state is
the fully interacting ground state is
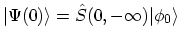 . The state at
. The state at
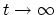 must be
defined carefully. If the interactions remain on, then this state is not well
described by the non-interacting ground state. Alternatively, one could require
that the interactions are turned off at large times, which returns the system
to the ground-state
must be
defined carefully. If the interactions remain on, then this state is not well
described by the non-interacting ground state. Alternatively, one could require
that the interactions are turned off at large times, which returns the system
to the ground-state
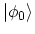 .
.
SCHWINGER [92] suggested another method of handling the asymptotic
limit
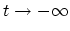 . He proposed that the time integral in the
. He proposed that the time integral in the 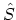 operator has two parts; one goes from
operator has two parts; one goes from
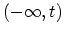 while the second goes
from
while the second goes
from
 . The integration path is a contour, which starts and
ends at
. The integration path is a contour, which starts and
ends at 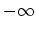 . The advantage of this method is that one starts
and ends the
. The advantage of this method is that one starts
and ends the 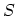 operator expansion with a known state
operator expansion with a known state
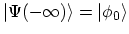 . Instead of the time-ordering
operator (B.21), a contour-ordering operator can be employed. The
contour-ordering operator
. Instead of the time-ordering
operator (B.21), a contour-ordering operator can be employed. The
contour-ordering operator
 orders the time labels according to
their order on the contour
orders the time labels according to
their order on the contour  . Under equilibrium condition the
contour-ordered method gives results that are identical to the time-ordered
method described in Section 3.1.1. The main advantage of the
contour-ordered method is in describing non-equilibrium phenomena using
GREEN's functions. Non-equilibrium theory is entirely based upon this
formalism, or equivalent methods.
. Under equilibrium condition the
contour-ordered method gives results that are identical to the time-ordered
method described in Section 3.1.1. The main advantage of the
contour-ordered method is in describing non-equilibrium phenomena using
GREEN's functions. Non-equilibrium theory is entirely based upon this
formalism, or equivalent methods.
Any operator
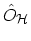 in the HEISENBERG picture can be transformed into the
interaction picture (see (B.13))
in the HEISENBERG picture can be transformed into the
interaction picture (see (B.13))
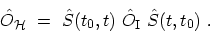 |
(3.19) |
Analogous to the derivation of (B.24), it can be shown that the
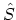 operator is given by
operator is given by
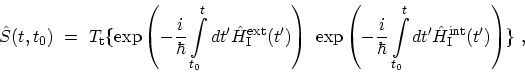 |
(3.20) |
where the operators are in the interaction representation. The ordinary
time-ordering can also be written as ordering along contour branches 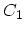 and
and 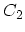 as depicted in Fig. 3.1
as depicted in Fig. 3.1
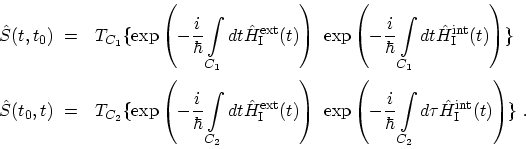 |
(3.21) |
By combining two contour branches,
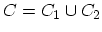 ,
(3.19) can be rewritten as
,
(3.19) can be rewritten as
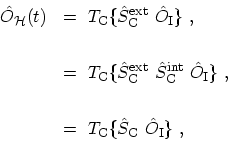 |
(3.22) |
where,
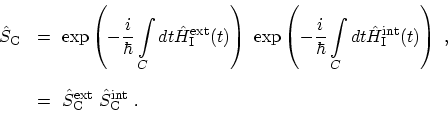 |
(3.23) |
Figure 3.1:
The contour
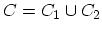 runs
on the real axis, but for clarity its two branches
runs
on the real axis, but for clarity its two branches 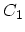 and
and 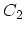 are
shown slightly away from the real axis. The contour
are
shown slightly away from the real axis. The contour 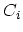 runs from
runs from
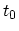 to
to
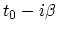 .
.
|
|
In equation (3.17)
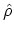 describes the
equilibrium state of the system before the external perturbation
describes the
equilibrium state of the system before the external perturbation
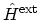 is turned on. Interactions
is turned on. Interactions
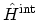 , which
are switched on adiabatically at
, which
are switched on adiabatically at 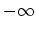 , are present in
, are present in
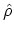 . However, to apply WICK's theorem (Section 3.4.1), one has to work with
non-interacting operators. A methodology similar to the MATSUBARA theory can
be applied to express the many-particle density operator
. However, to apply WICK's theorem (Section 3.4.1), one has to work with
non-interacting operators. A methodology similar to the MATSUBARA theory can
be applied to express the many-particle density operator
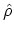 in
terms of the single-particle density operator
in
terms of the single-particle density operator
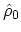 ,
see Appendix B.5. If the contour
,
see Appendix B.5. If the contour
![$ {C_i}=[t_0,t_0-i\beta]$](img526.png) is chosen (Fig. 3.1), then (B.34) takes the form
is chosen (Fig. 3.1), then (B.34) takes the form
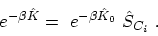 |
(3.24) |
Therefore, (3.17) can be rewritten as
![$\displaystyle \langle \hat{O}_\mathscr{H}(t) \rangle \ = \frac{\mathrm{Tr}[e^{-...
...}_\mathscr{H}(t) ]}
{\mathrm{Tr}[e^{-\beta \hat{K}_0}T_{C_i}\hat{S}_{C_i}]}\ ,$](img528.png) |
(3.25) |
Using the relations (3.22) and
(3.25), the GREEN's function
in (3.18) becomes [196]
![\begin{displaymath}\begin{array}{l}\displaystyle
G({\bf {r}},t,{\bf {r'}},t') \...
...}_0}T_{C_i} \hat{S}_{C_i}\ T_{C} \hat{S}_{C}]} \ .
\end{array}\end{displaymath}](img529.png) |
(3.26) |
The twofold expansion of the density operator and the field operators
may conveniently be combined to a single expansion. The two contours 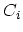 and
and 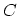 can be combined together,
can be combined together,
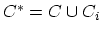 (Fig. 3.2), and a contour-ordering operator
(Fig. 3.2), and a contour-ordering operator
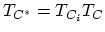 , which orders along
, which orders along 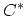 , can be introduced. Hence, a
point on
, can be introduced. Hence, a
point on 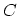 is always earlier than a point on
is always earlier than a point on 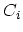 . Furthermore, we
define an interaction representation with respect to
. Furthermore, we
define an interaction representation with respect to 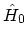 on
on 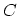 and
with respect to
and
with respect to 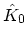 on
on 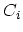 . Therefore, the GREEN's function
in (3.18) is given by
. Therefore, the GREEN's function
in (3.18) is given by
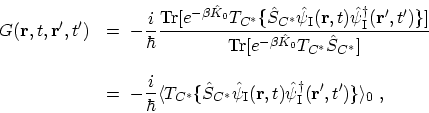 |
(3.27) |
where
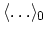 represents the statistical average with respect
to
represents the statistical average with respect
to
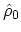 . From here we assume that all statistical averages are with
respect to
. From here we assume that all statistical averages are with
respect to
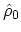 and drop the 0 from the brackets
and drop the 0 from the brackets
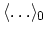 .
.
Figure 3.2:
The contour
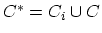 , runs
from
, runs
from 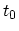 to
to 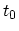 and from
and from 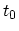 to
to
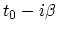 .
.
|
|
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() . He proposed that the time integral in the
. He proposed that the time integral in the ![]() operator has two parts; one goes from
operator has two parts; one goes from
![]() while the second goes
from
while the second goes
from
![]() . The integration path is a contour, which starts and
ends at
. The integration path is a contour, which starts and
ends at ![]() . The advantage of this method is that one starts
and ends the
. The advantage of this method is that one starts
and ends the ![]() operator expansion with a known state
operator expansion with a known state
![]() . Instead of the time-ordering
operator (B.21), a contour-ordering operator can be employed. The
contour-ordering operator
. Instead of the time-ordering
operator (B.21), a contour-ordering operator can be employed. The
contour-ordering operator
![]() orders the time labels according to
their order on the contour
orders the time labels according to
their order on the contour ![]() . Under equilibrium condition the
contour-ordered method gives results that are identical to the time-ordered
method described in Section 3.1.1. The main advantage of the
contour-ordered method is in describing non-equilibrium phenomena using
GREEN's functions. Non-equilibrium theory is entirely based upon this
formalism, or equivalent methods.
. Under equilibrium condition the
contour-ordered method gives results that are identical to the time-ordered
method described in Section 3.1.1. The main advantage of the
contour-ordered method is in describing non-equilibrium phenomena using
GREEN's functions. Non-equilibrium theory is entirely based upon this
formalism, or equivalent methods.
![]() in the HEISENBERG picture can be transformed into the
interaction picture (see (B.13))
in the HEISENBERG picture can be transformed into the
interaction picture (see (B.13))
![\includegraphics[width=.5\textwidth]{figures/Contour_Re_Im_1.eps}](img524.png)
![]() describes the
equilibrium state of the system before the external perturbation
describes the
equilibrium state of the system before the external perturbation
![]() is turned on. Interactions
is turned on. Interactions
![]() , which
are switched on adiabatically at
, which
are switched on adiabatically at ![]() , are present in
, are present in
![]() . However, to apply WICK's theorem (Section 3.4.1), one has to work with
non-interacting operators. A methodology similar to the MATSUBARA theory can
be applied to express the many-particle density operator
. However, to apply WICK's theorem (Section 3.4.1), one has to work with
non-interacting operators. A methodology similar to the MATSUBARA theory can
be applied to express the many-particle density operator
![]() in
terms of the single-particle density operator
in
terms of the single-particle density operator
![]() ,
see Appendix B.5. If the contour
,
see Appendix B.5. If the contour
![]() is chosen (Fig. 3.1), then (B.34) takes the form
is chosen (Fig. 3.1), then (B.34) takes the form