3.4 Perturbation Expansion of the GREEN's Function
In previous sections GREEN's functions at zero and finite temperatures have
been defined. It was shown that the GREEN's functions can be written in terms
of the 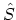 operator
operator
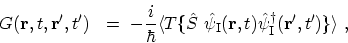 |
(3.28) |
where  includes the effects of interactions and external perturbations
includes the effects of interactions and external perturbations
 |
(3.29) |
Unfortunately, it is not possible to give an analytical solution for
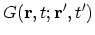 , unless the interaction perturbation
, unless the interaction perturbation
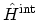 is set equal to zero. This gives the non-interacting
GREEN's function (see Appendix D)
is set equal to zero. This gives the non-interacting
GREEN's function (see Appendix D)
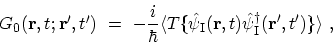 |
(3.30) |
which is central for any perturbation expansion.
This section proceeds the calculation of the GREEN's function by expanding the
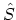 operator as series of products of
operator as series of products of
 in the numerator and the denominator. By expanding the
in the numerator and the denominator. By expanding the 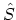 operator one obtains (see (B.20))
operator one obtains (see (B.20))
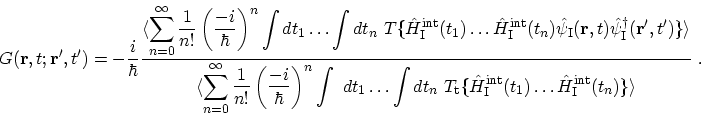 |
(3.31) |
The expansion of the numerator of the GREEN's function
in (3.31) can be written as
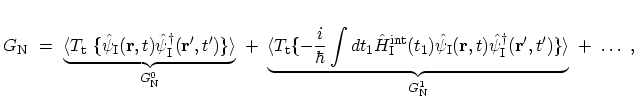 |
(3.32) |
where the superscript denotes the order of perturbation. The zero-order
perturbation leads to non-interacting GREEN's function
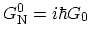 . WICK's theorem allows us to write each of these brackets in terms of
non-interacting GREEN's function and the interaction potential. The same procedure can
be applied to the denominator. The terms in the expansion of the denominator,
. WICK's theorem allows us to write each of these brackets in terms of
non-interacting GREEN's function and the interaction potential. The same procedure can
be applied to the denominator. The terms in the expansion of the denominator,
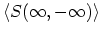 , are called vacuum polarization
terms [191].
, are called vacuum polarization
terms [191].
Different expansion terms achieved from the WICK theorem can be translated
into FEYNMAN diagrams (Appendix E). FEYNMAN introduced the idea of
representing different contributions obtained from the WICK decomposition by
drawings. These drawings, called diagrams, are very useful for providing an
insight into the physical processes which these terms represent. The
FEYNMAN diagrams provide an illustrative way to solve many-body problems
and the perturbation expansion of GREEN's functions.
Subsections
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() operator as series of products of
operator as series of products of
![]() in the numerator and the denominator. By expanding the
in the numerator and the denominator. By expanding the ![]() operator one obtains (see (B.20))
operator one obtains (see (B.20))