3.4.2 First-Order Perturbation Expansion
The electron-electron interaction up to the first-order perturbation is studied
here. In the interaction representation the operator corresponding to this
kind of interaction is given by
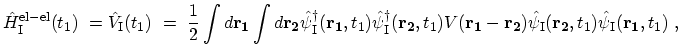 |
(3.35) |
where the COULOMB interaction potential is assumed to be an instantaneous
potential proportional to a delta function
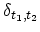 . The first-order term of the
perturbation expansion is given by
. The first-order term of the
perturbation expansion is given by
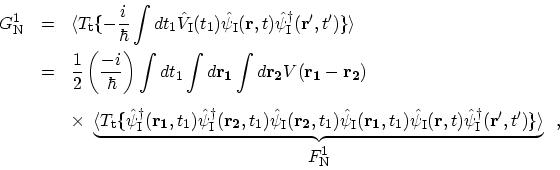 |
(3.36) |
![\begin{displaymath}\begin{array}{ll}
F^1_\mathrm{N} \ = \ [&+\langle
T_\mathr...
...}_\mathrm{I}^\dagger({\bf {r'}},t')\}\rangle\ ]\ .
\end{array}\end{displaymath}](img558.png) |
(3.37) |
By replacing the brackets by GREEN's functions one gets
![\begin{displaymath}\begin{array}{lll}
G^{1}_\mathrm{N} & = & \displaystyle \fra...
..._{0}({\bf {r_{1}}},t_{1};{\bf {r'}},t')}_{(f)}]\ .
\end{array}\end{displaymath}](img559.png) |
(3.38) |
Figure 3.4:
FEYNMAN diagrams of the first-order
perturbation terms
 .
.
|
FEYNMAN diagrams for the corresponding terms are shown
in Fig. 3.4. In the first-order example the connected diagrams 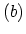 and
and
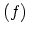 are equal, as are the diagrams
are equal, as are the diagrams 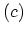 and
and 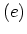 ; they differ only in that
the integration variables
; they differ only in that
the integration variables
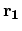 and
and
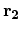 are
interchanged, whereas the COULOMB potential is symmetric under this
substitution. It is therefore sufficient to retain just one diagram of each
type, simultaneously omitting the factor
are
interchanged, whereas the COULOMB potential is symmetric under this
substitution. It is therefore sufficient to retain just one diagram of each
type, simultaneously omitting the factor 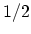 in front
of (3.38). For the
in front
of (3.38). For the 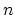 th-order perturbation there are
th-order perturbation there are 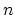 ! possible
interchanges of integration variables. Therefore, the repetition of the
same diagrams cancels the factor
! possible
interchanges of integration variables. Therefore, the repetition of the
same diagrams cancels the factor 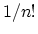 in (3.31).
in (3.31).
Diagram 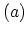 and
and 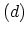 contain sub-units that
are not connected by any lines to the rest of the diagram.
Feynman diagrams in which all parts are not connected are called
disconnected diagrams.
Equation (3.38) shows that such diagrams are typically have GREEN's
function and interactions whose arguments close on themselves. As a result the
contribution of this sub-unit can be factored out of the expression for
contain sub-units that
are not connected by any lines to the rest of the diagram.
Feynman diagrams in which all parts are not connected are called
disconnected diagrams.
Equation (3.38) shows that such diagrams are typically have GREEN's
function and interactions whose arguments close on themselves. As a result the
contribution of this sub-unit can be factored out of the expression for
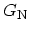 . The same procedure can be applied for the denominator.
In this cases, the second term of the expansion includes only two non-vanishing terms
which are only disconnected diagrams of (3.38), namely (a) and (d).
. The same procedure can be applied for the denominator.
In this cases, the second term of the expansion includes only two non-vanishing terms
which are only disconnected diagrams of (3.38), namely (a) and (d).
![\begin{displaymath}\begin{array}{lll}
G^{1}_\mathrm{D} & = & \displaystyle
\fr...
..._{0}({\bf {r_{1}}},t_{1};{\bf {r_{2}}},t_{1})]\ ,
\end{array}\end{displaymath}](img572.png) |
(3.39) |
As a result, these terms cancel the disconnected diagrams of the numerator and
the resulting GREEN's function consists of only connected diagrams. It can be
shown that in general the vacuum polarization terms cancel the disconnected
diagrams in the expansion of the GREEN's function [204].
As a result the GREEN's function is just the summation of all topologically
different connected diagrams [185]
![\begin{displaymath}\begin{array}{l}
G({\bf {r}},t;{\bf {r'}},t') = \\ [10pt]\ \...
...hrm{I}({\bf {r'}},t')\}
\rangle_\mathrm{conn} \ .
\end{array}\end{displaymath}](img573.png) |
(3.40) |
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() and
and ![]() contain sub-units that
are not connected by any lines to the rest of the diagram.
Feynman diagrams in which all parts are not connected are called
disconnected diagrams.
Equation (3.38) shows that such diagrams are typically have GREEN's
function and interactions whose arguments close on themselves. As a result the
contribution of this sub-unit can be factored out of the expression for
contain sub-units that
are not connected by any lines to the rest of the diagram.
Feynman diagrams in which all parts are not connected are called
disconnected diagrams.
Equation (3.38) shows that such diagrams are typically have GREEN's
function and interactions whose arguments close on themselves. As a result the
contribution of this sub-unit can be factored out of the expression for
![]() . The same procedure can be applied for the denominator.
In this cases, the second term of the expansion includes only two non-vanishing terms
which are only disconnected diagrams of (3.38), namely (a) and (d).
. The same procedure can be applied for the denominator.
In this cases, the second term of the expansion includes only two non-vanishing terms
which are only disconnected diagrams of (3.38), namely (a) and (d).