For certain applications in classical transport theory it is advantageous to write the BOLTZMANN equation as
an integral equation, rather than an integro-differential equation. An
analogous situation holds in quantum kinetics. Instead of working with the
KADANOFF-BAYM equations (3.62) and (3.63), it may
be useful to consider their integral forms. Historically,
KELDYSH [202] derived his alternative form almost simultaneously
and independently of KADANOFF and BAYM. However, the KELDYSH and
KADANOFF-BAYM formalisms are equivalent.
By applying LANGRETH's rules to the DYSON equation (3.44) one obtains
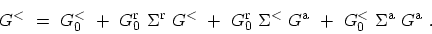 |
(3.66) |
For convenience a notation where a product of two terms is interpreted as a
matrix product in the internal variables (space, time, etc.) has been used.
One can proceed by iteration with respect to 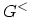 . Iterating once, and
regrouping the terms one obtains
. Iterating once, and
regrouping the terms one obtains
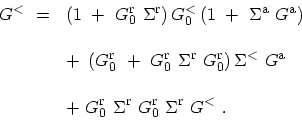 |
(3.67) |
The form of (3.67) suggests that infinite order iterations results
in [185]
 |
(3.68) |
Equation (3.68) is equivalent to KELDYSH's results. In the original
work, however, it was written for another function,
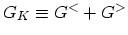 . This
difference is only of minor significance [185].
. This
difference is only of minor significance [185].
The first term on the right hand-side of (3.68) accounts for the
initial conditions. One can show that this term vanishes for steady-state
systems, if the system was in a non-interacting state in the infinite
past [185]. Thus, in many applications it is sufficient to only
keep the second term.
Similar steps can be followed to obtain the kinetic equation for 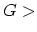 . In
integral form these equations can be written as
. In
integral form these equations can be written as
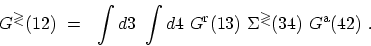 |
(3.69) |
The relation between the KELDYSH equation and the KADANOFF-BAYM equation is
analogous to the relation between an ordinary differential equation plus a
boundary condition and the corresponding integral equation.
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() . In
integral form these equations can be written as
. In
integral form these equations can be written as