4.1 Electrostatic Potential and the POISSON Equation
Planar CNT-FETs constitute the majority of devices fabricated to date, mostly
due to their relative simplicity and moderate compatibility with existing
manufacturing technologies. However, coaxial devices (see Fig. 4.1) are
of special interest because their geometry allows for better electrostatic control
than their planar counterparts. These devices would exhibit
wrap-around gates that maximize capacitive
coupling between the gate electrode and the CNT channel. Presently, the closest
approximation to this geometry are electrolyte-gated
devices [232,233]. Alternative structures that place CNTs
vertically with respect to the substrate have already been used for
field-emission applications [234,235]. Coaxial CNT-FETs could
be fashioned by placing CNTs inside the cavities of a porous material
such as alumina, surrounding them by gate electrodes.
Figure 4.1:
Schematic of the coaxial CNT-FET.
|
|
Appropriate treatment of the electrostatic potential in the device
is essential for accurately predicting the device characteristics [236].
The electron-electron interaction self-energy of lowest order yields
the HARTREE potential, which is the solution of the POISSON equation
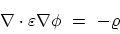 |
(4.1) |
where 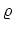 is the total charge density, given (in cylindrical coordinates) by
[237]
is the total charge density, given (in cylindrical coordinates) by
[237]
![\begin{displaymath}\begin{array}{l} \displaystyle \varrho \ = \ \frac{\mathrm{q}[p(z)-n(z)]\delta(r-r_\mathrm{CNT})}{2\pi r} \ . \end{array}\end{displaymath}](img722.png) |
(4.2) |
Here, 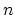 and
and 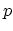 denote the electron and hole concentration per unit length,
respectively, and
denote the electron and hole concentration per unit length,
respectively, and
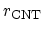 is the radius of the CNT. In (4.2)
is the radius of the CNT. In (4.2)
 is the DIRAC delta function in cylindrical coordinates, implying
that the carrier density is approximated by a sheet charge distributed
along the insulator-CNT interface [237]. Due to azimuthal symmetry
in wrap-around gate devices, the carriers are uniformly distributed as
a function of the azimuthal angle.
is the DIRAC delta function in cylindrical coordinates, implying
that the carrier density is approximated by a sheet charge distributed
along the insulator-CNT interface [237]. Due to azimuthal symmetry
in wrap-around gate devices, the carriers are uniformly distributed as
a function of the azimuthal angle.
Subsections
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors