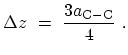4.3 Tight-Binding HAMILTONian
The general form of the tight-binding HAMILTONian for electrons in a CNT can be written as
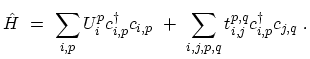 |
(4.13) |
The sum is taken over all rings  ,
,  along the transport direction, which
is assumed to be the
along the transport direction, which
is assumed to be the 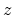 -direction of the cylindrical coordinate system, and over all
atomic locations
-direction of the cylindrical coordinate system, and over all
atomic locations 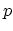 ,
,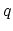 in a ring. We use a nearest-neighbor tight-binding
in a ring. We use a nearest-neighbor tight-binding
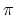 -bond model [243,10]. Each atom in an
-bond model [243,10]. Each atom in an
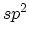 -coordinated CNT has three nearest neighbors, located
-coordinated CNT has three nearest neighbors, located
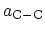 away. The band-structure consists of
away. The band-structure consists of 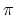 -orbitals only, with the hopping
parameter
-orbitals only, with the hopping
parameter
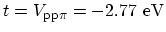 and zero on-site potential.
Furthermore, it is assumed that the electrostatic
potential
and zero on-site potential.
Furthermore, it is assumed that the electrostatic
potential 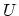 rigidly shifts the on-site potentials. Such a tight-binding
model is adequate to model transport properties in un-deformed CNTs.
rigidly shifts the on-site potentials. Such a tight-binding
model is adequate to model transport properties in un-deformed CNTs.
In this work we consider zigzag CNTs. However, this method can be readily
extended to armchair or chiral CNTs. Within the nearest-neighbor
approximation, only the following parameters are
non zero [10]
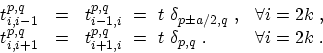 |
(4.14) |
Figure 4.6 shows that a zigzag CNT is composed of rings (layers)
of 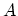 - and
- and 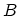 -type carbon atoms, where
-type carbon atoms, where 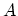 and
and 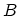 represent the
two carbon atoms in a unit cell of graphene. Each A-type ring is
adjacent to a B-type ring. Within nearest-neighbor tight-binding
approximation the total HAMILTONian matrix is block tri-diagonal [243]
represent the
two carbon atoms in a unit cell of graphene. Each A-type ring is
adjacent to a B-type ring. Within nearest-neighbor tight-binding
approximation the total HAMILTONian matrix is block tri-diagonal [243]
![$\displaystyle \ensuremath{{\underline{H}}} = { \left[ \begin{array}{cccccc} \en...
...underline{H}}}_5 & \bullet\\ & & & & \bullet & \bullet \end{array} \right]} \ ,$](img774.png) |
(4.15) |
where the diagonal blocks,
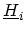 , describe the coupling within an
A-type or B-type carbon ring and off-diagonal blocks,
, describe the coupling within an
A-type or B-type carbon ring and off-diagonal blocks,
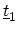 and
and
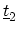 , describe the coupling between adjacent rings.
It should be noted that the odd numbered HAMILTONian
, describe the coupling between adjacent rings.
It should be noted that the odd numbered HAMILTONian
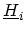 refer to A-type rings
and the even numbered one to B-type rings. Each A-type ring couples to the
next B-type ring according to
refer to A-type rings
and the even numbered one to B-type rings. Each A-type ring couples to the
next B-type ring according to
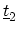 and to the previous B-type ring
according to
and to the previous B-type ring
according to
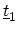 . Each B-type ring couples to the next A-type ring
according to
. Each B-type ring couples to the next A-type ring
according to
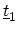 and to the previous A-type ring according to
and to the previous A-type ring according to
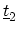 .
In a
.
In a 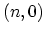 zigzag CNT, there are
zigzag CNT, there are 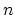 carbon atoms in each ring, thus, all the
sub-matrices in (4.15) have a size of
carbon atoms in each ring, thus, all the
sub-matrices in (4.15) have a size of 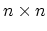 .
.
In the nearest-neighbor tight binding approximation, carbon atoms within a ring
are not coupled to each other so that
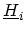 is a diagonal matrix. The
value of a diagonal entry is the potential at that carbon atom site. In the
case of a coaxially gated CNT, the potential is constant along the CNT
circumference. As a result, the sub-matrices
is a diagonal matrix. The
value of a diagonal entry is the potential at that carbon atom site. In the
case of a coaxially gated CNT, the potential is constant along the CNT
circumference. As a result, the sub-matrices
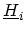 are given by the
potential at the respective carbon ring times the identity matrix
are given by the
potential at the respective carbon ring times the identity matrix
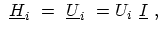 |
(4.16) |
Figure 4.6:
Layer layout of a
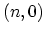 zigzag CNT. Circles are rings of A-type carbon atoms and squares
rings of B-type carbon atoms. The coupling coefficient
between nearest neighbor carbon atoms is
zigzag CNT. Circles are rings of A-type carbon atoms and squares
rings of B-type carbon atoms. The coupling coefficient
between nearest neighbor carbon atoms is 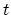 . The coupling matrices
between rings are denoted by
. The coupling matrices
between rings are denoted by
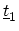 and
and
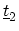 , where
, where
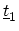 is a diagonal matrix and
is a diagonal matrix and
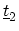 is non-diagonal.
is non-diagonal.
|
|
There are two types of coupling matrices between nearest carbon rings,
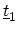 and
and
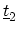 . As shown in Fig. 4.6, the first type,
. As shown in Fig. 4.6, the first type,
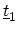 , only couples an A(B) carbon atom to its B(A) counterpart in the
neighboring ring. The coupling matrix is just the tight-binding coupling
parameter times an identity matrix,
, only couples an A(B) carbon atom to its B(A) counterpart in the
neighboring ring. The coupling matrix is just the tight-binding coupling
parameter times an identity matrix,
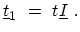 |
(4.17) |
The second type of coupling matrix,
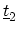 , couples an A(B) atom to two
B(A) neighbors in the adjacent ring. The coupling matrix is
, couples an A(B) atom to two
B(A) neighbors in the adjacent ring. The coupling matrix is
![$\displaystyle \ensuremath{{\underline{t}}}_2\ = \ { \left[ \begin{array}{cccccc...
... & \\ \displaystyle & t & t & \\ & & \bullet & \bullet \end{array} \right]} \ .$](img783.png) |
(4.18) |
The period of the zigzag CNT in the longitudinal direction contains four rings,
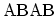 , and has a length of
, and has a length of
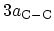 . Therefore, the average distance
between the rings is
. Therefore, the average distance
between the rings is
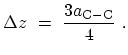 |
(4.19) |
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
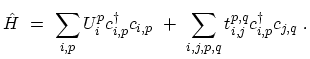
![]() is a diagonal matrix. The
value of a diagonal entry is the potential at that carbon atom site. In the
case of a coaxially gated CNT, the potential is constant along the CNT
circumference. As a result, the sub-matrices
is a diagonal matrix. The
value of a diagonal entry is the potential at that carbon atom site. In the
case of a coaxially gated CNT, the potential is constant along the CNT
circumference. As a result, the sub-matrices
![]() are given by the
potential at the respective carbon ring times the identity matrix
are given by the
potential at the respective carbon ring times the identity matrix
![\includegraphics[width=0.35\textwidth]{figures/TB-CNT.eps}](img779.png)
![]() and
and
![]() . As shown in Fig. 4.6, the first type,
. As shown in Fig. 4.6, the first type,
![]() , only couples an A(B) carbon atom to its B(A) counterpart in the
neighboring ring. The coupling matrix is just the tight-binding coupling
parameter times an identity matrix,
, only couples an A(B) carbon atom to its B(A) counterpart in the
neighboring ring. The coupling matrix is just the tight-binding coupling
parameter times an identity matrix,
![]() , and has a length of
, and has a length of
![]() . Therefore, the average distance
between the rings is
. Therefore, the average distance
between the rings is