4.4 Mode-Space Transformation
A mode space approach
significantly reduces the size of the HAMILTONian
matrix [9]. Due to quantum confinement along the CNT
circumference, circumferential modes appear and transport can be described in terms
of these modes. If 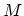 modes contribute to transports, and if
modes contribute to transports, and if 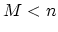 , then the size of
the problem is reduced from
, then the size of
the problem is reduced from 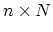 to
to
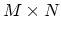 , where
, where 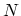 is number of carbon rings along the CNT. If
the potential profile does not vary sharply along the CNT, subbands are
decoupled [9] and one can solve
is number of carbon rings along the CNT. If
the potential profile does not vary sharply along the CNT, subbands are
decoupled [9] and one can solve 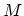 one-dimensional problems of
size
one-dimensional problems of
size 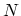 .
.
Mathematically, one performs a basis transformation on the HAMILTONian of the 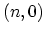 zigzag
CNT to decouple the problem into
zigzag
CNT to decouple the problem into 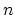 one-dimensional mode space lattices [243]
one-dimensional mode space lattices [243]
![\begin{displaymath}\begin{array}{ll} \ensuremath{{\underline{H}}}^{'} \ &\displa...
...] & & & & \bullet & \bullet \end{array} \right]} \ ,\end{array}\end{displaymath}](img790.png) |
(4.20) |
with
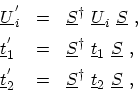 |
(4.21) |
where
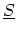 is the transformation matrix from the real space basis to the
mode space basis. The purpose is to decouple the modes after the
basis transformation, i.e., to make the HAMILTONian matrix blocks between
different modes equal to zero. This requires that after the transformation,
the matrices
is the transformation matrix from the real space basis to the
mode space basis. The purpose is to decouple the modes after the
basis transformation, i.e., to make the HAMILTONian matrix blocks between
different modes equal to zero. This requires that after the transformation,
the matrices
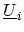 ,
,
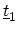 , and
, and
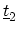 , become diagonal. Since
, become diagonal. Since
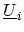 and
and
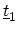 are identity matrices multiplied by a constant, they
remain unchanged and diagonal after any basis transformation,
are identity matrices multiplied by a constant, they
remain unchanged and diagonal after any basis transformation,
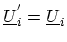 and
and
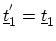 .
To diagonalize
.
To diagonalize
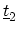 , elements of the transformation matrix
, elements of the transformation matrix
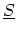 have to be the eigen-vectors of
have to be the eigen-vectors of
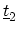 . These eigen-vectors are plane
waves with wave-vectors satisfying the periodic boundary condition around the
CNT. The eigen-values are
. These eigen-vectors are plane
waves with wave-vectors satisfying the periodic boundary condition around the
CNT. The eigen-values are
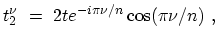 |
(4.22) |
where
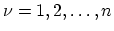 [243]. The phase factor in (4.22) has no
effect on the results such as charge and current density, thus it can be
omitted and
[243]. The phase factor in (4.22) has no
effect on the results such as charge and current density, thus it can be
omitted and
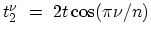 can be used instead.
can be used instead.
Figure 4.7:
Zigzag
CNT and the corresponding one-dimensional chain with two sites per unit
cell with hopping parameters 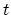 and
and
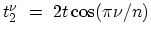 .
.
|
|
After the basis transformation all sub-matrices,
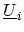 ,
,
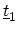 , and
, and
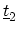 are diagonal. By reordering the basis according to
the modes, the HAMILTONian matrix takes the form
are diagonal. By reordering the basis according to
the modes, the HAMILTONian matrix takes the form
![$\displaystyle \ensuremath{{\underline{H}}}^{'} \ = \ { \left[ \begin{array}{ccc...
...h{{\underline{H}}}^\nu & & \\ [1.5pt] & & & & \bullet & \end{array} \right]}\ ,$](img800.png) |
(4.23) |
where
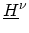 is the HAMILTONian matrix for the
is the HAMILTONian matrix for the 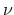 th mode [243]
th mode [243]
![$\displaystyle \ensuremath{{\underline{H}}}^\nu = { \left[ \begin{array}{cccccc}...
...\\ & & & t & U_5 & \bullet\\ & & & & \bullet & \bullet \end{array} \right]} \ .$](img802.png) |
(4.24) |
The one-dimensional tight-binding HAMILTONian 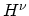 describes a chain of atoms
with two sites per unit cell and on-site potential
describes a chain of atoms
with two sites per unit cell and on-site potential 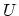 and hopping parameters
and hopping parameters 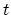 and
and 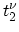 (Fig. 4.7). The spatial grid used for device simulation
corresponds to the circumferential rings of carbon atoms. Therefore, the rank
of the matrices for each subband are equal to the total number of these rings
(Fig. 4.7). The spatial grid used for device simulation
corresponds to the circumferential rings of carbon atoms. Therefore, the rank
of the matrices for each subband are equal to the total number of these rings 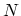 .
Self-energies can be also transformed into mode space
.
Self-energies can be also transformed into mode space
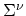 , see Section 4.5
and Section 4.6. The GREEN's functions can therefore be defined for
each subband (mode) and one can solve the system of transport equations for each subband
independently
, see Section 4.5
and Section 4.6. The GREEN's functions can therefore be defined for
each subband (mode) and one can solve the system of transport equations for each subband
independently
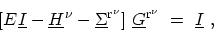 |
(4.25) |
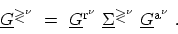 |
(4.26) |
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() zigzag
CNT to decouple the problem into
zigzag
CNT to decouple the problem into ![]() one-dimensional mode space lattices [243]
one-dimensional mode space lattices [243]
![\includegraphics[width=0.38\textwidth]{figures/TB-CNT-Mod.eps}](img799.png)
![]() ,
,
![]() , and
, and
![]() are diagonal. By reordering the basis according to
the modes, the HAMILTONian matrix takes the form
are diagonal. By reordering the basis according to
the modes, the HAMILTONian matrix takes the form
![$\displaystyle \ensuremath{{\underline{H}}}^{'} \ = \ { \left[ \begin{array}{ccc...
...h{{\underline{H}}}^\nu & & \\ [1.5pt] & & & & \bullet & \end{array} \right]}\ ,$](img800.png)