There is a variety of methods available for numerical adaptive
integration [247]. Adaptive strategies divide the integration
interval into sub-intervals and, typically, employ a progressive formula in
each sub-interval with some fixed upper limit on the number of points. If the
required accuracy is not achieved by the progressive formula, the sub-interval
is bisected and a similar procedure carried out on each half. This
sub-division process is carried out recursively until the desired accuracy is
achieved. An obvious way to obtain an error estimate is based on the
comparison between two quadrature approximations [248]. However, due to the
dependence of such procedures on the underlying integration formulae, this
method may not be reliable [249]. Error
estimation with sequences of null rules has been proposed as a simple
solution [250]. In adaptive quadrature algorithms the error
estimate governs the decision on whether to accept the current approximation
and terminate or to continue. Therefore, both the efficiency and the
reliability depend on the error estimation algorithm. The decision to further
subdivide a region may be based on either local or global information.
Local information refers only to the region being currently processed, while
global information refers obviously to data concerning all
regions. Integration programs based on global subdivision strategies are more
efficient and reliable [251].
In this work a global error estimator based on the null rules method has been
employed [249]. The efficiency of this method is studied for the LORENTZian
function (4.60). Figure 4.13-a shows the
number of required energy grid points for an interval
![$ \mathrm{[-1,1]~eV}$](img905.png) versus the relative error
versus the relative error 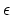 of the integration. The required number
of energy grid points versus the width of the resonance,
of the integration. The required number
of energy grid points versus the width of the resonance, 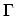 , is shown
Fig. 4.13-b. To resolve a very narrow
resonance (
, is shown
Fig. 4.13-b. To resolve a very narrow
resonance (
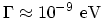 ) with a very high
accuracy (
) with a very high
accuracy (
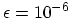 ) only a few hundred grid
points (
) only a few hundred grid
points (
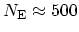 ) are required.
) are required.
Figure 4.13:
a) shows the number of
required energy grid points versus the maximum desired relative error,
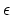 , in the adaptive integration method. b) shows the number of
required energy grid points versus the width of the resonance,
, in the adaptive integration method. b) shows the number of
required energy grid points versus the width of the resonance,
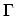 . The LORENTZian function (4.60) is used as a
reference.
. The LORENTZian function (4.60) is used as a
reference.
|
|
Figure 4.14:
The left figure shows the
normalized spectrum of the carrier concentration in a Schottky type CNT-FET.
The right figure shows the spectrum of the carrier
concentration in the middle of the device for the energy range shown by the
arrow. The results achieved from the adaptive and non-adaptive method are
compared. With the aid of the adaptive method narrow and close resonances
are resolved with a total number of
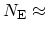 1000 energy grid
points, whereas the non-adaptive method misses some resonances
with the same number of energy grid points.
1000 energy grid
points, whereas the non-adaptive method misses some resonances
with the same number of energy grid points.
|
|
Figure 4.14 shows the normalized spectrum of the carrier concentration in
a Schottky type CNT-FET (see Section 2.8.2). The length of the device is
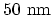 . Energy barriers at the metal-CNT interfaces cause
longitudinal confinement in the tube. Since the device is quite long, the
spacing between confined states is very small. In CNTs the electron-phonon
interaction is rather weak and the confining SCHOTTKY barriers are thick,
such that resonances are only weakly broadened, (see Chapter 5).
Due to phonon absorption
and emission processes there will be more resonances compared to the
ballistic case. In this case, if a non-adaptive method is employed the
numerical error in the calculation of the carrier concentration can be
large. The right part of Fig. 4.14 compares the results achieved
from the adaptive and non-adaptive methods. The relative error in the
electron density of the non-adaptive method reaches up to
. Energy barriers at the metal-CNT interfaces cause
longitudinal confinement in the tube. Since the device is quite long, the
spacing between confined states is very small. In CNTs the electron-phonon
interaction is rather weak and the confining SCHOTTKY barriers are thick,
such that resonances are only weakly broadened, (see Chapter 5).
Due to phonon absorption
and emission processes there will be more resonances compared to the
ballistic case. In this case, if a non-adaptive method is employed the
numerical error in the calculation of the carrier concentration can be
large. The right part of Fig. 4.14 compares the results achieved
from the adaptive and non-adaptive methods. The relative error in the
electron density of the non-adaptive method reaches up to 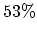 in the middle of the device.
in the middle of the device.
In [252] the resonant states have been determined by an eigenvalue
solver for finding the roots of the characteristic equation. However, this
method has several drawbacks. Due to the non-linearity introduced by the
self-energies, a non-linear eigenvalue solver has to be employed. Usually
non-linear solvers are based on NEWTON's method. Using a non-linear solver for
each iteration can increase the simulation time severely and introduce
additional convergence problems. For example, most solvers fail to find narrow
resonances located closely to each other. The output of the solver is the
energy position and the width of the resonance, but not any information about
the shape of the resonance. In general the shape of resonances deviates from
the ideal LORENTZian shape. The grid has to be allocated based on an initial
guess. This implies that the accuracy of the calculated carrier concentration
can not be predefined and strongly depends on the how close the initial guess
is to the actual solution. With the adaptive method the discussed problems do
not occur.
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() versus the relative error
versus the relative error ![]() of the integration. The required number
of energy grid points versus the width of the resonance,
of the integration. The required number
of energy grid points versus the width of the resonance, ![]() , is shown
Fig. 4.13-b. To resolve a very narrow
resonance (
, is shown
Fig. 4.13-b. To resolve a very narrow
resonance (
![]() ) with a very high
accuracy (
) with a very high
accuracy (
![]() ) only a few hundred grid
points (
) only a few hundred grid
points (
![]() ) are required.
) are required.
![\includegraphics[width=\textwidth]{figures/NE-Tol-Gamma.eps}](img909.png)
![\includegraphics[width=\textwidth]{figures/CNT-RhoA.eps}](img910.png)