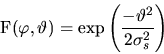Prev: 6.2 Low-Pressure Processes

6.2.1 Reactive Ion Etching

The etching effect during reactive ion etching is characterized by the simultaneous impact of ions and neutrals. According to their charge state, the behavior of ions and neutrals is different and they interact differently with the surface.

The surface attack of neutrals is of chemical nature. It is similar to wet etching and represents an isotropic contribution to the etch rate. The distributions of neutrals can be described with cosine or sub-cosine functions, since the chargeless neutral particles experience no acceleration in electric fields.

A different situation is given for ions. Due to their charge they become accelerated in an electric field. This results in two effects. The first one is a strong directionality of their distributions, which can be described by a Gaussian distribution

$${\mathrm F}(\varphi, \vartheta) = \exp \left(\frac{-\vartheta^2}{2 \sigma_s^2}\right)$$ (6.13)

with the standard deviation $\sigma_s$. The second effect is the physical attack of the surface caused by the high kinetic energy of the accelerated ions. Moreover the ions enhance the etching effect of the neutrals, since their physical attack leads to strong surface damage creating new reaction sites for the chemical attack by the neutrals.

According to the basic derivations from Section 6.1.4 and the above considerations the rate equation sums up to

$$r_\mathrm{rie} = \frac{r_0}{\mathrm{N}}\int \limits_{2\pi} [ \mathrm{F}^\mathrm{ions}(\varphi, \vartheta)$$

$$+ \mathrm{F}^\mathrm{neutrals}(\varphi, \vartheta) (1 + \mathrm{E... ...) \Omega(\varphi,\vartheta) d\Omega )] \Omega(\varphi,\vartheta) d\Omega$$ (6.14)

which assumes a unity sticking coefficient and therefore no reflections. $\mathrm{E}$ is the parameter which assesses the amount of the enhancement in the attack of neutrals in presence of surface attack by ions.

It is beyond the scope of this illustrative example to derive a complete hierarchy of models for the great variety of plasma assisted etching processes applied in semiconductor manufacturing. In addition, the lack of comprehensive experimental data would make this task an academic exercise with restricted applicability. Nevertheless, since the assignment of the parameters of the model allows a flexible transition from chemically to physically driven process conditions, the applications of the proposed approach range from plasma enhanced chemical dry etching processes to reactive ion etching (RIE) processes with predominant physical etching. With the assessment and the calibration of the model parameters the reactive ion etching model can be applied to processes for spacer formation, trench capacitors for DRAM cells, and trenches for shallow trench isolations.

Figure 6.13: Reactive ion etching of trenches with different widths.

Fig. 6.13 shows the simulation result for two STI structures with different trench widths. The distribution for the neutrals was set to $\cos(a\vartheta)^b$, with $a=2$ and $b=1.5$. (6.13) with a standard deviation of $\sigma_s=5^\circ$ was chosen for the distribution of ions. A moderate ion enhancement factor $\mathrm{E}=1$ was assumed. The etch rate for the silicon substrate was 4nm/min and the etching time was 400s. The etch rate of the mask was set to 0 assuming a very high selectivity between the silicon substrate and the resist polymer, which leads to a negligible etch attack of the mask.

The width of the mask opening for the wider trench is 0.4$\mu\mathrm m$, following rather conservative design rules, for the narrower trench it was set to 0.1$\mu\mathrm m$. For the same process conditions and the same etching time, the etching depth for the wider trench is significantly higher than for the 0.1$\mu\mathrm m$ trench. This is due to the aperture effect, where the wider mask opening allows a higher amount of incident particles, provoking the stronger erosion.

Prev: 6.2 Low-Pressure Processes