

Next: 3.2.11.2 Hydrodynamic Impact Ionization
Up: 3.2.11 Impact Ionization
Previous: 3.2.11 Impact Ionization
In the DD approximation the generation rates are usually calculated as:
| |
|
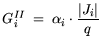 |
(3.63) |
with i = n,p and introduced into the continuity equation as:
| |
|
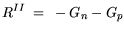 |
(3.64) |
In a very straight forward model, e.g. for the use in diodes, the impact ionization rates can be modeled according
to:
| |
|
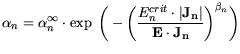 |
(3.65) |
and
| |
|
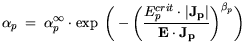 |
(3.66) |
This approach is very well known and widely used to compile the
different sets of data suggested by the experiments.
A number of sets, obtained from various measurement approaches,
are summarized in Table 3.26.
Table 3.26:
Impact Ionization parameters in bulk III-V binary
semiconductors, diode: pn-diode measurements, MC: Monte Carlo simulation.
| Material |
E |
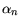 |
E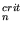 |
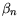 |
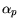 |
E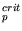 |
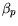 |
Extraction |
References |
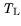 , N , N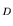 |
[V/cm] |
[cm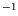 ] ] |
[V/cm] |
|
[cm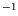 ] ] |
[V/cm] |
|
|
|
| GaAs |
|
2.99e5 |
6.848e5 |
1.6 |
2.215e5 |
6.57e5 |
1.75 |
diode |
[55] |
| |
|
2.2e5 |
6.66e5 |
1.52 |
2.16e5 |
7.03e5 |
1.56 |
diode |
[221] |
| AlAs |
|
3.69e5 |
1.43e6 |
1.33 |
1.99e5 |
1.21e6 |
1.56 |
diode |
[221] |
| InAs |
|
|
|
|
|
|
|
|
|
| 77 K |
5e4-3e5 |
1.09e5 |
9.8e4 |
1 |
- |
- |
- |
MC |
[91] |
| 300 K |
5e4-2.5e5 |
2.46e5 |
9.16e4 |
1 |
- |
- |
- |
MC |
[91] |
| 300 K |
5e3-1e5 |
1.25e5 |
3.6e4 |
1 |
- |
- |
- |
MC |
[52] |
| InP |
|
|
|
|
|
|
|
|
|
| 1.2e15 |
2.4-3.6e5 |
1.12e7 |
3.11e6 |
1 |
4.79e6 |
2.55e6 |
1 |
diode |
[67] |
| 3.0e16 |
3.6-5.6e5 |
2.93e6 |
2.64e6 |
1 |
1.62e6 |
2.11e6 |
1 |
diode |
[67] |
| 1.2e17 |
5.3-7.7e5 |
2.32e5 |
8.46e5 |
2 |
2.48e5 |
7.89e5 |
2 |
diode |
[67] |
| GaN |
2-4.05e6 |
1.4e7 |
1.48e7 |
1.40 |
2.95e5 |
5.17e6 |
2 |
MC |
[200] |
| |
3-3.75e6 |
8.9e6 |
1.05e7 |
2 |
- |
- |
- |
MC |
[149] |
|
In order to sort and qualify these, the extraction procedure is additionally named.
The direct comparison of the model parameters is rendered complicated, since the parameters 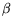 are not always used for fitting and set to 1. However, principal tendencies can be observed.
A relatively stable database is available for GaAs. The value for AlAs is found from fitting of the material composition of Al
are not always used for fitting and set to 1. However, principal tendencies can be observed.
A relatively stable database is available for GaAs. The value for AlAs is found from fitting of the material composition of Al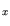 Ga
Ga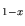 As
for
As
for 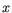 = 0..0.6. For InAs, the soft onset of impact ionization cannot be modeled very well with equations (3.68) and (3.69). Thus, the
fit is only valid for the range of the electric field indicated in Table 3.26. However, some observations can be made which are the low
breakdown field and the positive
temperature coefficient of the InAs parameters. For InP the doping dependence can be evaluated, which reduces impact ionization for higher impurity
concentrations. For GaN only preliminary data are available for comparably higher fields than for the GaAs based materials.
The high critical fields extracted show the breakdown hardness
of this materials system due to the large band gap.
= 0..0.6. For InAs, the soft onset of impact ionization cannot be modeled very well with equations (3.68) and (3.69). Thus, the
fit is only valid for the range of the electric field indicated in Table 3.26. However, some observations can be made which are the low
breakdown field and the positive
temperature coefficient of the InAs parameters. For InP the doping dependence can be evaluated, which reduces impact ionization for higher impurity
concentrations. For GaN only preliminary data are available for comparably higher fields than for the GaAs based materials.
The high critical fields extracted show the breakdown hardness
of this materials system due to the large band gap.
Parameters for different material compositions of
ternary compounds from the above basic materials are listed in
Table 3.27. For most of the compositions of
Al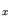 Ga
Ga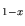 As and for In
As and for In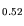 Al
Al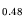 As
measurements are available. The data from [297] and
[309] has been used for HEMT simulation in
[281].
As
measurements are available. The data from [297] and
[309] has been used for HEMT simulation in
[281].
Table 3.27:
Impact ionization parameters in bulk III-V ternary
semiconductors.
| Material |
Mat. Comp. |
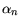 |
E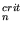 |
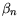 |
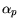 |
E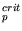 |
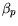 |
Extraction |
References |
| |
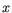 |
[cm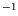 ] ] |
[V/cm] |
|
[cm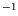 ] ] |
[V/cm] |
|
|
|
| AlGaAs |
0.1 |
1.81e5 |
6.31e5 |
2 |
3.05e5 |
7.22e5 |
1.9 |
diode |
[232] |
| |
0.15 |
2.17e5 |
7.74e5 |
1.533 |
2.51e5 |
8.60e5 |
1.516 |
diode |
[221] |
| |
0.2 |
1.09e6 |
1.37e6 |
1.3 |
6.45e5 |
1.11e6 |
1.5 |
diode |
[232] |
| |
0.3 |
2.21e5 |
7.64e5 |
2.0 |
2.79e5 |
8.47e5 |
1.9 |
diode |
[232] |
| |
0.3 |
2.69e5 |
9.54e5 |
1.476 |
3.20e5 |
1.06e6 |
1.43 |
diode |
[221] |
| |
0.4 |
1.74e7 |
3.39e6 |
1.0 |
3.06e6 |
2.07e6 |
1.2 |
diode |
[232] |
| |
0.6 |
2.95e7 |
1.16e8 |
1.44 |
3.11e5 |
1.215e6 |
1.433 |
diode |
[221] |
| InGaAs |
0.53 |
5.9e5 |
1.33e6 |
1 |
1e6 |
1.63e6 |
1 |
diode |
[205] |
| |
0.53 |
6.9e4 |
9e5 |
1 |
1.15e6 |
1.7e6 |
1 |
diode |
[297] |
| InAlAs |
0.52 |
7.36e4 |
5.62e5 |
2 |
1.57e4 |
4.88e5 |
2 |
diode |
[59] |
| |
0.52 |
8.6e6 |
3.5e6 |
1 |
2.3e7 |
4.5e6 |
1 |
diode |
[309] |
| InGaP |
0.48 |
4.57e5 |
1.413e6 |
1.73 |
4.73e5 |
1.425e6 |
1.65 |
diode |
[102] |
| |
0.5 |
3.85e6 |
3.71e6 |
1 |
1.71e6 |
3.195e6 |
1 |
diode |
[97] |
|
For those data sets which were presented consistently
for various material compositions, the following formulae are
applied to model the material dependence of the impact ionization
parameters.The extracted parameters for Al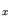 Ga
Ga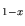 As are
given in Table 3.28 and shown in Fig. 3.16, where a
systematic material dependence can be observed.
As are
given in Table 3.28 and shown in Fig. 3.16, where a
systematic material dependence can be observed.
| |
|
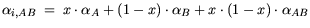 |
(3.67) |
| |
|
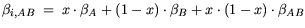 |
(3.68) |
| |
|
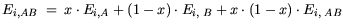 |
(3.69) |
Table 3.28:
Impact ionization parameters for the model in bulk
III-V ternary semiconductors [221].
| Material |
Valid for 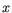 |
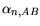 |
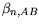 |
E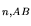 |
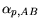 |
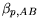 |
E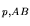 |
Refs. |
| |
|
[cm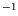 ] ] |
|
[V/cm] |
[cm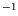 ] ] |
|
[V/cm] |
|
Al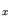 Ga Ga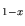 As As |
0-0.6 |
-5.1e4 |
1.44 |
1.75e5 |
4.45e4 |
-0.54 |
8.66e5 |
[221] |
|
Figure 3.16:
Impact ionization parameters as a
function of material composition for Al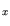 Ga
Ga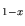 As
[221].
As
[221].
|
Figure 3.17:
Impact ionization rates as a
function of material composition for In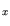 Al
Al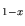 As
[60,91,221,309].
As
[60,91,221,309].
|
Fig. 3.17 shows the data available for the typical
barrier material In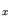 Al
Al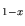 As. The experimental situation for In
As. The experimental situation for In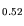 Al
Al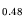 As is indicated.
The plot is useful for the modeling of different material compositions in metamorphic HEMTs.
For InAs MC data from [91] are taken.
For AlAs data from the extraction in Table 3.28 are assumed.
As is indicated.
The plot is useful for the modeling of different material compositions in metamorphic HEMTs.
For InAs MC data from [91] are taken.
For AlAs data from the extraction in Table 3.28 are assumed.
For HEMT simulation it is extremely desirable to model
the temperature dependence of the impact ionization rates for
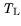
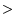 300 K in order to understand the interaction between
electrically and thermally induced device and performance
degeneration. Unfortunately, very little data are available to
extract the dependence for the layer materials
In
300 K in order to understand the interaction between
electrically and thermally induced device and performance
degeneration. Unfortunately, very little data are available to
extract the dependence for the layer materials
In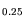 Ga
Ga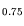 As and In
As and In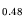 Al
Al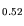 As. For
In
As. For
In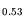 Ga
Ga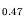 As in [193] a positive temperature
coefficient was reported resulting in increasing impact
ionization with rising
As in [193] a positive temperature
coefficient was reported resulting in increasing impact
ionization with rising
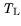 . Fig. 3.18 shows the
dependence in GaAs for electron and holes, where impact
ionization decreases as function of
. Fig. 3.18 shows the
dependence in GaAs for electron and holes, where impact
ionization decreases as function of
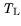 .
In Fig. 3.19 the extracted model parameters
from a consistent set of measurement data from [285] for
InP are given versus temperature. The data for
.
In Fig. 3.19 the extracted model parameters
from a consistent set of measurement data from [285] for
InP are given versus temperature. The data for
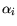 and
and
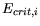 , also presented in Table 3.29, show a
systematic increase of the critical field versus
, also presented in Table 3.29, show a
systematic increase of the critical field versus
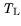 .
. 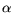 first rises and drops above a certain
first rises and drops above a certain
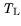 . However, the overall
temperature coefficient of the impact ionization rates is negative
for the temperatures observed. Recently, measurement data for
Al
. However, the overall
temperature coefficient of the impact ionization rates is negative
for the temperatures observed. Recently, measurement data for
Al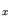 Ga
Ga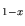 As were published [326], very
unfortunately, the paper contains several inconsistencies in data
and comparisons applied.
As were published [326], very
unfortunately, the paper contains several inconsistencies in data
and comparisons applied.
Figure 3.18:
Impact ionization parameters
versus temperature for a given field in GaAs [60].
|
Figure 3.19:
Impact ionization parameters
versus temperature in InP [285].
|
Table 3.29 gives data sets compiled in the form of (3.68) and (3.69).
Table 3.29:
Measured impact ionization parameters for InP as a function of lattice temperature.
| Material |
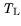 |
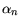 |
E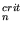 |
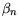 |
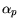 |
E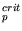 |
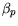 |
| |
[K] |
[cm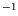 ] ] |
[V/cm] |
|
[cm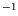 ] ] |
[V/cm] |
|
| InP |
298 |
9.2e6 |
3.44e6 |
1 |
4.3e6 |
2.72e6 |
1 |
| |
373 |
1.22e7 |
3.73e6 |
1 |
1.06e7 |
3.36e6 |
1 |
| |
398 |
1.026e7 |
3.78e6 |
1 |
1.39e7 |
3.63e6 |
1 |
| |
448 |
1.04e7 |
3.89e6 |
1 |
1.06e7 |
3.56e6 |
1 |
|
To obtain a more systematic view of the temperature
dependence also for other materials the following approach is
used: In [64] Chau and Pavlidis compiled available sets of
data, as given in the previous section, into the Okuto-Crowell
model [202]. The Baraff approach [26] is used
there with its lattice temperature dependence to establish a base
for an estimate of impact ionization data at unknown temperatures
and material compositions. A similar approach is taken here for
such materials which have a similar temperature dependence as
GaAs, i.e., Al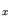 Ga
Ga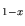 As, and InP. Contrary
to [64] this work does not include In
As, and InP. Contrary
to [64] this work does not include In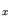 Ga
Ga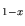 As
for
As
for 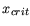
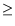 0.53, where the temperature coefficient is
positive, as was shown in [75,193]. An even lower
bound for this critical In content
0.53, where the temperature coefficient is
positive, as was shown in [75,193]. An even lower
bound for this critical In content 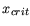 , where the
temperature coefficient of InGaAs changes its sign, is discussed
in Chapter 7.
, where the
temperature coefficient of InGaAs changes its sign, is discussed
in Chapter 7.
The Okuto-Crowell impact ionization model basically is a modification of (3.68) and (3.69), where three parameters
enter the formula:
| |
|
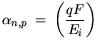 exp exp![$\displaystyle \bigg(0.217\bigg(\frac{E_i}{E_r}\bigg)^{1.14}- \bigg\{\bigg[ 0.21...
...\bigg)^{1.14}\bigg]^2 +\bigg(\frac{E_i}{qF\lambda}\bigg)^2 \bigg\}^{0.5} \bigg)$](img539.gif) |
(3.70) |
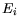 is a threshold energy,
is a threshold energy, 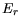 is the average energy loss per scattering, and
is the average energy loss per scattering, and 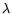 the mean free path
for the optical phonon scattering. The temperature dependence of (3.73) is introduced in (3.74)
and (3.75).
the mean free path
for the optical phonon scattering. The temperature dependence of (3.73) is introduced in (3.74)
and (3.75).
| |
|
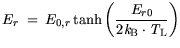 |
(3.71) |
| |
|
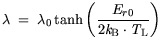 |
(3.72) |
Model parameters are compiled in Table 3.30. The
data given include the modifications as stated by Chau and
Pavlidis in [64]. Thus, for the materials used in this
work a systematic scheme is found to fill the gaps of the data
base as function of temperature. This presents a consistent
approach to the lattice temperature dependence to support the
modeling in the hydrodynamic model in the next section.
Table 3.30:
Impact ionization rates according to the modeling
approach.
| Material |
 |
Composition |
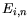 |
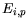 |
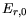 |
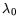 |
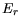 |
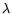 |
| |
|
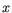 |
[eV] |
|
[meV] |
Å |
[meV] |
Å |
| GaAs |
n,p |
- |
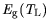 +0.52 +0.52 |
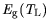 +0.7 +0.7 |
43 |
60.65 |
29.3 |
50 |
| InP |
n,p |
- |
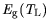 +0.16 +0.16 |
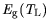 -0.21 -0.21 |
52.15 |
56.6 |
39.9 |
45.2 |
Al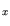 Ga Ga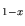 As As |
n,p |
0.1 |
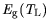 +0.18 +0.18 |
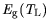 +0.31 +0.31 |
45.12 |
53 |
31.7 |
40.9 |
| |
n,p |
0.2 |
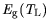 +0.51 +0.51 |
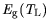 +0.64 +0.64 |
47.1 |
54.17 |
34 |
42.3 |
| |
n,p |
0.3 |
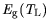 +0.68 +0.68 |
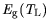 +0.86 +0.86 |
48.06 |
55.6 |
35.1 |
44 |
| |
n,p |
0.4 |
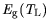 +0.69 +0.69 |
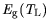 +0.94 +0.94 |
50.45 |
55.95 |
37.9 |
44.4 |
In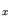 Al Al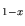 As As |
n,p |
0.52 |
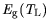 +0.71 +0.71 |
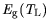 +1.31 +1.31 |
45.37 |
45.45 |
32 |
32 |
|


Next: 3.2.11.2 Hydrodynamic Impact Ionization
Up: 3.2.11 Impact Ionization
Previous: 3.2.11 Impact Ionization
Quay
2001-12-21
![]() Ga
Ga![]() As and for In
As and for In![]() Al
Al![]() As
measurements are available. The data from [297] and
[309] has been used for HEMT simulation in
[281].
As
measurements are available. The data from [297] and
[309] has been used for HEMT simulation in
[281].
![]() Ga
Ga![]() As are
given in Table 3.28 and shown in Fig. 3.16, where a
systematic material dependence can be observed.
As are
given in Table 3.28 and shown in Fig. 3.16, where a
systematic material dependence can be observed.
![\includegraphics[width=10 cm]{D:/Userquay/Promotion/HtmlDiss/fig-16.eps}](img529.gif)
![\includegraphics[width=10 cm]{D:/Userquay/Promotion/HtmlDiss/fig-16a.eps}](img530.gif)
![]() Al
Al![]() As. The experimental situation for In
As. The experimental situation for In![]() Al
Al![]() As is indicated.
The plot is useful for the modeling of different material compositions in metamorphic HEMTs.
For InAs MC data from [91] are taken.
For AlAs data from the extraction in Table 3.28 are assumed.
As is indicated.
The plot is useful for the modeling of different material compositions in metamorphic HEMTs.
For InAs MC data from [91] are taken.
For AlAs data from the extraction in Table 3.28 are assumed.
![]()
![]() 300 K in order to understand the interaction between
electrically and thermally induced device and performance
degeneration. Unfortunately, very little data are available to
extract the dependence for the layer materials
In
300 K in order to understand the interaction between
electrically and thermally induced device and performance
degeneration. Unfortunately, very little data are available to
extract the dependence for the layer materials
In![]() Ga
Ga![]() As and In
As and In![]() Al
Al![]() As. For
In
As. For
In![]() Ga
Ga![]() As in [193] a positive temperature
coefficient was reported resulting in increasing impact
ionization with rising
As in [193] a positive temperature
coefficient was reported resulting in increasing impact
ionization with rising
![]() . Fig. 3.18 shows the
dependence in GaAs for electron and holes, where impact
ionization decreases as function of
. Fig. 3.18 shows the
dependence in GaAs for electron and holes, where impact
ionization decreases as function of
![]() .
In Fig. 3.19 the extracted model parameters
from a consistent set of measurement data from [285] for
InP are given versus temperature. The data for
.
In Fig. 3.19 the extracted model parameters
from a consistent set of measurement data from [285] for
InP are given versus temperature. The data for
![]() and
and
![]() , also presented in Table 3.29, show a
systematic increase of the critical field versus
, also presented in Table 3.29, show a
systematic increase of the critical field versus
![]() .
. ![]() first rises and drops above a certain
first rises and drops above a certain
![]() . However, the overall
temperature coefficient of the impact ionization rates is negative
for the temperatures observed. Recently, measurement data for
Al
. However, the overall
temperature coefficient of the impact ionization rates is negative
for the temperatures observed. Recently, measurement data for
Al![]() Ga
Ga![]() As were published [326], very
unfortunately, the paper contains several inconsistencies in data
and comparisons applied.
As were published [326], very
unfortunately, the paper contains several inconsistencies in data
and comparisons applied.
![\includegraphics[width=10 cm]{D:/Userquay/Promotion/HtmlDiss/fig-16i.eps}](img533.gif)
![\includegraphics[width=10 cm]{D:/Userquay/Promotion/HtmlDiss/fig-16j.eps}](img534.gif)
![]() Ga
Ga![]() As, and InP. Contrary
to [64] this work does not include In
As, and InP. Contrary
to [64] this work does not include In![]() Ga
Ga![]() As
for
As
for ![]()
![]() 0.53, where the temperature coefficient is
positive, as was shown in [75,193]. An even lower
bound for this critical In content
0.53, where the temperature coefficient is
positive, as was shown in [75,193]. An even lower
bound for this critical In content ![]() , where the
temperature coefficient of InGaAs changes its sign, is discussed
in Chapter 7.
, where the
temperature coefficient of InGaAs changes its sign, is discussed
in Chapter 7.