

Next: 3.3.3 The Insulator-Metal Interface
Up: 3.3 Boundary and Interface
Previous: 3.3.1.2 Thermionic Field Emission
The condition for the semiconductor-insulator interface
equivalently is determined by a continuous potential and by an
applied surface charge density
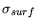 according to the
Gauß law:
according to the
Gauß law:
| |
|
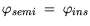 |
(3.95) |
| |
|
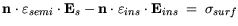 |
(3.96) |
The carrier flux and the carrier energy flux are zero.
The lattice temperature
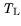 is continuous. To
describe the Fermi level pinning at the surface due to a high
density of states for traps, distributed surfaces charges are
introduced which describe the surface depletion due to the band
bending. The current densities
is continuous. To
describe the Fermi level pinning at the surface due to a high
density of states for traps, distributed surfaces charges are
introduced which describe the surface depletion due to the band
bending. The current densities
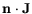 and
the energy fluxes
and
the energy fluxes
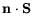 are set to zero.
are set to zero.
Quay
2001-12-21
![]() according to the
Gauß law:
according to the
Gauß law: