

Next: 5.1.2 Factor Extraction
Up: 5.1 Statistical Analysis of
Previous: 5.1 Statistical Analysis of
A wafer map can be formalized by looking at
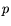 different random variables X
different random variables X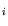 which form p-dimen-
which form p-dimen-
sional
random vector 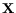 =
=
![$ [X_1,X_2,...,X_p]$](img768.gif) . Every component
. Every component
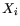 can take values n values, where n is equal to the overall
number of cells. The mean values of the components are given by:
can take values n values, where n is equal to the overall
number of cells. The mean values of the components are given by:
| |
|
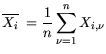 |
(5.1) |
while the standard deviations
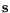 =
=
![$ [s_1,s_2,...,s_p]$](img772.gif) ,[115], read:
,[115], read:
| |
|
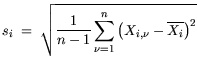 |
(5.2) |
Fig. 5.2 shows the results of a DC-RF wafer
map of a 4 inch GaAs PHEMT wafer in order to demonstrate the
method. Typical DC and small-signal quantities are used that
define the vector 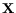 .
.
Figure 5.2:
4 inch wafer map results of a
pseudomorphic AlGaAs/InGaAs HEMT.
|
The covariance matrix 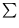 with the components:
with the components:
| |
|
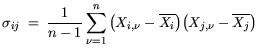 |
(5.3) |
and the correlation matrix 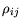 :
:
| |
|
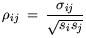 |
(5.4) |
are normally not considered for analysis.
Table C.1 in Appendix C shows the correlation
matrix of the example data set shown in Fig. 5.2.
Measures are taken to test whether the chosen variables in the
wafer map are suitable for factor analysis, as described in
[22,53]. A significance test is performed to
investigate the error probability, whether the variables are
uncorrelated. The significance is related to high values of the
correlation itself, as can be seen in Table C.1. Only
for correlation coefficients close to unity (i.e., 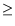 0.7)
there is a statistically significant probability of correlation,
which is not accidental. Further tests can be performed, such as
the Barlett test of spericity [22], which in our
example confirms the overall correlation of the data set, so that
further analysis is relevant. Third, the so-called
anti-image of the covariance and correlation matrix is calculated
[22,53]. This assumes that in general the
correlation coefficients
0.7)
there is a statistically significant probability of correlation,
which is not accidental. Further tests can be performed, such as
the Barlett test of spericity [22], which in our
example confirms the overall correlation of the data set, so that
further analysis is relevant. Third, the so-called
anti-image of the covariance and correlation matrix is calculated
[22,53]. This assumes that in general the
correlation coefficients 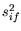 are composed as given
in (5.5).
are composed as given
in (5.5).
| |
|
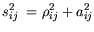 |
(5.5) |
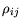 are the observed correlation coefficients
and
are the observed correlation coefficients
and 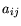 the so called partial correlation coefficients. The
anti-image controls how much of the observed variance can be
explained by a multiple regression analysis within the set of
observed variables. The partial correlation coefficients
the so called partial correlation coefficients. The
anti-image controls how much of the observed variance can be
explained by a multiple regression analysis within the set of
observed variables. The partial correlation coefficients 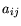 in (5.5) represent how much of the variance is
independent of the other variables in the data set, i.e.,
dependent on variables not contained in the data set. For the
computation, see [53].
This is necessary, since PCA assumes that common factors are the
source of variance for the variables X
in (5.5) represent how much of the variance is
independent of the other variables in the data set, i.e.,
dependent on variables not contained in the data set. For the
computation, see [53].
This is necessary, since PCA assumes that common factors are the
source of variance for the variables X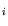 under investigation.
Another test for the data can be performed, which requires that
less than 25% of the non-diagonal elements in the anti-image
covariance matrix must be different form zero i.e. numerically,
under investigation.
Another test for the data can be performed, which requires that
less than 25% of the non-diagonal elements in the anti-image
covariance matrix must be different form zero i.e. numerically,
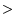 0.09. The example passes also this test, since none of the
components is
0.09. The example passes also this test, since none of the
components is 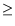 0.09. The two matrices are shown in
Table C.2 in Appendix C.
0.09. The two matrices are shown in
Table C.2 in Appendix C.
From the anti-image correlation matrix the Kaiser-Meyer-Olkin (
KMO) criterion
[53] can be obtained:
| |
|
KMO |
(5.6) |
where  are the observed correlation
coefficients and
are the observed correlation
coefficients and 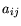 again the partial correlation
coefficients, i.e., contributions outside of the data set, as
separated in (5.5).
again the partial correlation
coefficients, i.e., contributions outside of the data set, as
separated in (5.5).
An overall KMO criterion close to unity means that the
data set is suitable for factor analysis.
For analysis of the contribution to (5.6), a measure of sampling adequacy
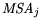 can be determined as:
can be determined as:
| |
|
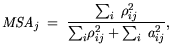 i i 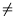 j j |
(5.7) |
This allows to analyze single variables for their usefulness in the factor analysis. For
the whole example the KMO reveals an average of 0.64, which is considered between mediocre and
middling on a scale between 0 and 1 established by Kaiser [22]. The variables
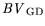 ,
,
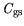 ,
,
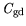
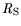 ,
,
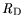 , and
, and
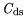 have
have 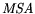 values of
values of 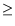 0.7 and are therefore further
used for analysis. The rest of the variables must be discarded as statistically insignificant.
Based on the significance information and the
0.7 and are therefore further
used for analysis. The rest of the variables must be discarded as statistically insignificant.
Based on the significance information and the  the whole procedure is repeated with the six
elements mentioned. The overall KMO criterion with the new reduced dataset reads KMO= 0.73, which
is middling according to Kaiser [22].
the whole procedure is repeated with the six
elements mentioned. The overall KMO criterion with the new reduced dataset reads KMO= 0.73, which
is middling according to Kaiser [22].


Next: 5.1.2 Factor Extraction
Up: 5.1 Statistical Analysis of
Previous: 5.1 Statistical Analysis of
Quay
2001-12-21
![]() different random variables X
different random variables X![]() which form p-dimen-
which form p-dimen-
![]() =
=
![]() . Every component
. Every component
![]() can take values n values, where n is equal to the overall
number of cells. The mean values of the components are given by:
can take values n values, where n is equal to the overall
number of cells. The mean values of the components are given by:
![]() can be determined as:
can be determined as: