| F = |
(2.38) |
Nearly all mutual interactions between oxidation and diffusion as well as several known side effects, e.g., OED (Oxidation Enhanced Diffusion), ORD (Oxidation Retarded Diffusion), are declared on basis of point defect models. The idea starts from the principle that at finite temperatures always a number of free lattice places (vacancies) and a belonging number of free atoms (interstitials) exist that influence the behavior of different dopant atoms in a definite manner. Today it is an established theory that not only the common used dopants (boron, arsenic, phosphorus, etc.) are diffusing via a pair diffusion mechanism but also the diffusion of oxygen is influenced by such effects where the movement of the atoms is mainly based on vacancy diffusion. Furthermore, at the interface between silicon and silicon dioxide silicon interstitials are generated and are injected into the silicon as well as into the silicon dioxide. These might increase the existing effects at the boundaries but the consequences are not yet fully declared.
A general accepted extension to the Model of Deal and Grove is the
model of Ho and Plummer [Nic82][Sch91] who described the enhancement of oxidation
with the availability of vacancies. They assumed that the
concentration can best be described by several charge states of the
vacancies which leads to an enhancement-factor concerning the linear
coefficient of Deal and Grove's model:
| F = |
(2.38) |
| CV = CV0 + CV+ |
(2.39) | ||
| CVi = CV0 + CV+ + CV- + CV- - | (2.40) |
n = 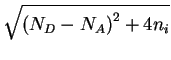
|
(2.41) |
The fitting parameter ![]() was found to
was found to
| (2.42) |