

Next: 3.2 Finite Boxes
Up: 3.1 Finite Elements
Previous: 3.1.2 Numerical Integration
The essence of the finite element method, already stated above, is to
approximate the unknown by an expression given as
where Ni are the interpolating shape functions prescribed in terms
of linear independent functions and ai are a set of unknown
parameters. Under normal circumstances the variables are chosen to be
identical with the values of the unknown function at the element
nodes, thus making
ui 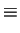 ai
ai |
|
|
(3.25) |
Now consider to interpolate a constant function over the simulation
domain. It is clear that a constant value of ai specified at all
nodes must result in a constant value of 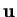 which immediately
implies that
which immediately
implies that
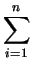 Ni = 1 Ni = 1 |
|
|
(3.26) |
at all points of the domain. The so defined shape functions are
referred to as standard shape functions and are the basics of
most finite element programs. Several extensions to the standard
shape functions exist and the reader is advised to relevant
literature [Sch80].
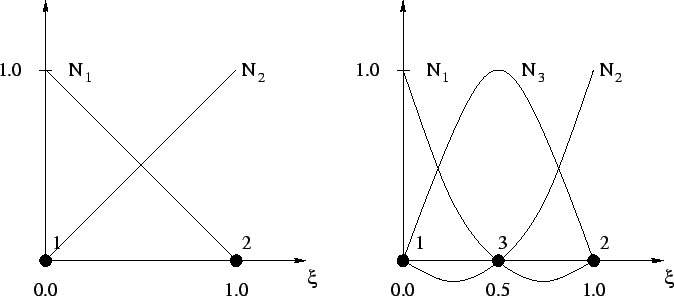
Figure 3.3:
Linear and quadratic shape functions for one-dimensional elements
|
|
The used interpolation scheme is illustrated in Fig. 3.3
where the node points have to be multiplied with the shape functions
to get the values inside the element. The order of interpolation of the
shape function stipulates the accuracy of the element. Thus, there are
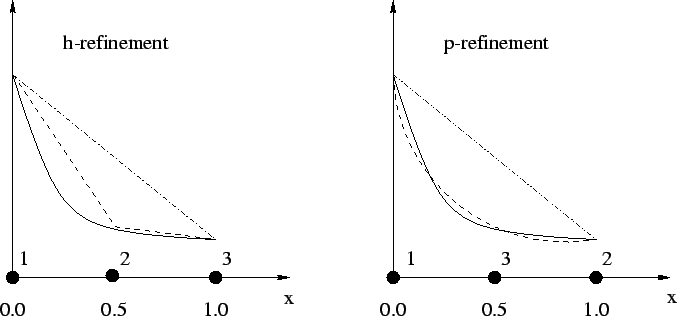
two strategies to get high quality results (Fig. 3.4):
- h-refinement: In this case the local density of elements is
increased that introduces a larger number of discrete points in the
areas of interest but the order of the interpolation function remains
unchanged. This version is often used due to the simpler approach but
especially in three dimensions the higher number of discrete points
is a serious drawback.
- p-refinement: Here, the order of the interpolation function
is increased so that the characteristics of approximation of the
element itself are better. This often reduces the amount of discrete
points that are needed to represent a given function within a
tolerable error level. Nevertheless, there are limits due to
oscillating results in case of higher orders. Therefore shape
functions up to a maximum order of three are normally used. For
further increase of accuracy the h-refinement seems to be the better
approach.
Figure 3.4:
Approximation characteristics of linear and quadratic shape functions
in case of h-refinement and p-refinement
|
|
The shape function itself can be calculated using a polynomial
approach. For linear interpolation on a one-dimensional element
with two nodes a polynomial of first order
can be used.
To calculate the coefficients 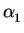 and
and 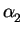 the values at the element nodes can be inserted into (3.27)
the values at the element nodes can be inserted into (3.27)
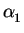 = u1
= u1 |
|
|
(3.28) |
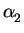 = - u1 + u2
= - u1 + u2 |
|
|
(3.29) |
Substituting these results into (3.27) yields
u(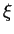 ) = u1(1 - ) = u1(1 - 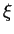 ) + u2 ) + u2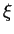 = u1N1(
= u1N1(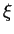 ) + u2N2( ) + u2N2(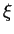 ) ) |
|
|
(3.30) |
The same principle can be used for all other orders of
interpolation as well as for different dimensions. For higher
orders of interpolation derivatives are additionally used to
calculate the coefficients of the polynomial.
For a summary of shape functions in one, two, and three dimensions
calculated for different interpolation orders refer to
Appendix B.


Next: 3.2 Finite Boxes
Up: 3.1 Finite Elements
Previous: 3.1.2 Numerical Integration
Mustafa Radi
1998-12-11
![]() which immediately
implies that
which immediately
implies that
