|
Using AMIGOS a new model has been developed based on the model of E. Rank [Ran90]. The key idea is the description of the local oxidation as a three component thermodynamic process involving silicon, silicon dioxide and oxidant molecules. This results in a reactive layer of finite width in contrast to the sharp interface between silicon and silicon dioxide in the conventional formulation. The numerical approximation takes advantage of this description in a finite element approach which models silicon, silicon dioxide and the reactive layer together, thus avoiding the necessity to track the interface with element edges. The smooth transition zone is a means to regularize the mathematical free boundary problem and can be selected in a way, that numerically seen, the same results appear as in case of sharp interface formulations. To distinguish between different materials a method similar to the level set method was chosen to keep the transition zone as small as possible (usually the transition zone is limited to a single element).
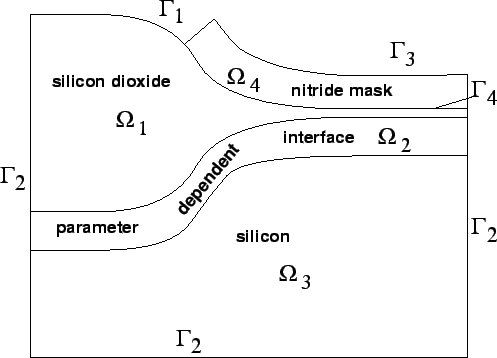
For the definition of the model consider Fig. 5.2 as
computation domain ![]() which consists of a pure silicon dioxide
range
which consists of a pure silicon dioxide
range ![]() , an interface range
, an interface range ![]() with a mixture of
silicon and silicon dioxide, a pure silicon range
with a mixture of
silicon and silicon dioxide, a pure silicon range ![]() and a
nitride mask
and a
nitride mask ![]() that is defined on a separate mesh and is connected
to
that is defined on a separate mesh and is connected
to ![]() via boundary
via boundary ![]() to transmit mechanical displacements.
For the nitride mask an elastic model is used to calculate its stress-strain
contribution. To describe the different phases of oxygen within the domain
to transmit mechanical displacements.
For the nitride mask an elastic model is used to calculate its stress-strain
contribution. To describe the different phases of oxygen within the domain
![]()
![]()
![]()
![]()
![]() a generation/recombination rate of oxygen
a generation/recombination rate of oxygen
f (ac, x) = 0.5 + 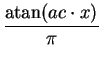 with ac with ac |
(5.21) |
The generation of silicon dioxide itself is handled by a generation rate:
The free oxidant diffusion in
![]()
![]()
![]()
![]()
![]() is
described by
is
described by
| (5.24) |
The mobility of oxygen is strongly influenced by the amount of the generated silicon dioxide since compounded oxygen atoms are assumed to be immobile. The amount of generated silicon dioxide itself depends on the local concentration of already generated oxide as well as of free oxygen which reacts with silicon immediately. This effect leads to an enhancement of oxidation at the very beginning, since nearly all oxide atoms are reacting with silicon. Later on, the reaction rate slows down due to the decreasing amount of reaction partners. Now, an increasing number of oxygen molecules must diffuse through the generated oxide layer towards the interface, before the molecules can finally be incorporated into the silicon and cause the interface movement. Furthermore, the so built-in oxygen involves a local stress which is imprinted into the system. In dependence of further treatment of the mechanical behavior a volume dilatation can be calculated.
The preferred approximation of mechanical behavior of silicon and
silicon dioxide can be reached by a visco-elastic model. Therefore, it
suggests itself to use a Maxwell body (Fig. 5.1) to solve
the mechanical equations. The advantage of the Maxwell body is, that
it can handle both extreme fields, elastic as well as viscous material
and of course a mixture of both - a visco-elastic behavior. Again,
the level set function ![]() (5.20) is used to distinguish
between different mechanical models:
(5.20) is used to distinguish
between different mechanical models:
The used strain relation is based on Hook's law (5.15)
that is expressed in a way that the dilatational components of stress,
which involve a volumetric expansion, and the deviatoric part, which
only accounts for shape modification, are decoupled. To account for
the nonlinear material behavior the modulus of rigidity G and
the compressibility ![]() are modeled as functions of
are modeled as functions of ![]() .
.
For the volumetric expansion we solve the equilibrium condition
| p = - |
(5.26) |
The stress histories have to be calculated in order to get a correct
stress-strain distribution within the different materials. Assuming
the model suggested in [Pen91] stress within elastic material is
calculated by
| (5.27) |
| (5.28) |