q . D . 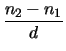 |
= |
(3.17) |
q . D . 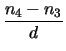 |
= |
(3.18) |
q . D . 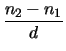 |
= |
(3.17) |
q . D . 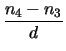 |
= |
(3.18) |
This equation system for n2 and n3 can be rewritten as
![\begin{figure}
\begin{center}
\includegraphics[width=10cm]{eps/1d-box.eps}
\end{center}\end{figure}](img303.gif) |
n1 and n4 are the fixed values of the carrier concentration on the left and the right boundary (Dirichlet boundary condition).
The characteristic polynomial of the system matrix is
The solutions of (3.20) are the eigenvalues of (3.19).
| = - |
(3.21) | |
| = - |
(3.22) |
According to (3.7) the spectral condition number of (3.19) is
| (3.23) |
and, therefore, for large ![]() the spectral condition of the system matrix
will be poor. Thus, if the internal state of a device results in a large value
of
the spectral condition of the system matrix
will be poor. Thus, if the internal state of a device results in a large value
of ![]() the solver cannot compute the solution of the linear system with
sufficient accuracy. The result will be an increase of iteration steps for the
Newton scheme, if convergence can be achieved at all.
the solver cannot compute the solution of the linear system with
sufficient accuracy. The result will be an increase of iteration steps for the
Newton scheme, if convergence can be achieved at all.
This problem can be alleviated by transforming the linear system
(3.19) as follows. Adding the second equation to the first
one and scaling the second equation with
![]()
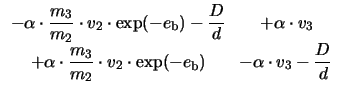
| |
= ![$\displaystyle \begin{array}{c}\displaystyle -\frac{D}{d}\cdot n_{1}\\ [2mm]\displaystyle -\frac{D}{d}\cdot n_{4}\end{array}$](img331.gif)
|
(3.24) |
results in the new system
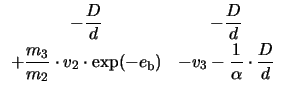
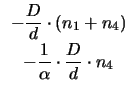
|
(3.25) |
The new system matrix has the eigenvalues
|
(3.26) |
hence, for large values of ![]() the spectral condition number
the spectral condition number
![]() is nearly independent of
is nearly independent of ![]() because in the limit for
because in the limit for
![]()
![]()
![]() the factors
the factors
![]() and
and
![]() are 1.
are 1.
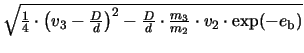 |
(3.27) |
The strong influence of the internal state of the device on the spectral condition of the equation system has been eliminated.