4.1.2 Principles of Finite Element Method

The basic idea of FEM is to discretize the domain of interest, where the PDE is defined, in order to obtain an approximate solution of the PDE by a linear combination of basis functions defined within each subdomain. Then, the assembly of subdomains, which is based on the process of putting the finite elements back into their original positions, results in a discrete set of equations which are analogous to the original mathematical problem.

The entire domain under investigation is approximated as an assembly of discrete elements, so-called finite elements, interconnected at points common to two or more elements, so-called nodes, as illustrated in (4.1). Each finite element is an independent geometric region of the domain over which equations with unknown variables of the given problem are defined using the governing equations of the mathematical model of interest.

Figure 4.1: Schematic view of the linear discretization of the domain in elements and nodes. The true solution is represented as a continuous function (dotted line) and the approximate solution is described as a piecewise polynomial (solid line).

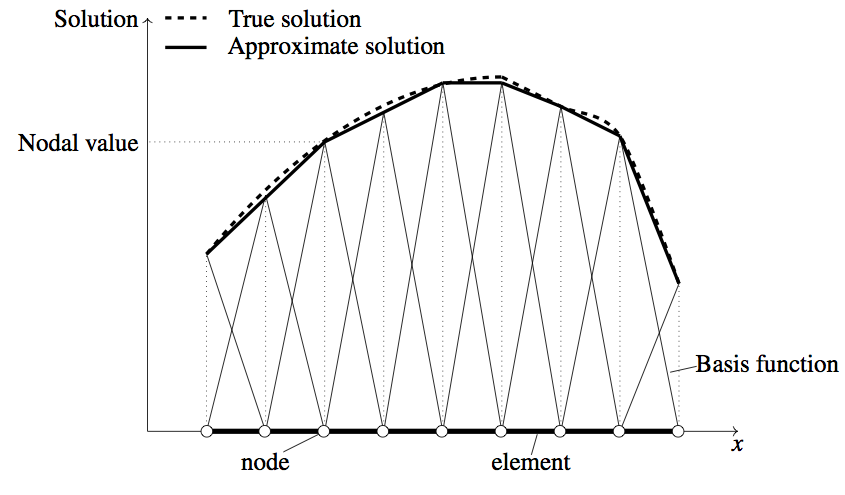In each finite element, these equations are solved by assuming basis functions which interpolate the unknown variables over the finite element, in order to approximate the solution of the problem within the element. The basis function is defined within the finite element using the values of the unknown variables at the nodes. The approximate solution to the problem within the element is obtained as a linear combination of nodal values of the variables and the basis functions for the element. The equations for the finite element relate the nodal values of the variables to other parameters. The formulation of the finite element analog of a model equation follows two main approaches, namely weighted-residual and weak formulation [116]. Then, with appropriate loadings, boundary, and initial conditions applied to the elements/nodes, the local element equations for all the finite elements are assembled together and solved simultaneously to obtain a continuous solution in terms of its values at the nodes.

During the finite element analysis, errors can be introduced due to the approximations of the domain discretization, the solutions of the element equations, and the solution of the assembled system of equations. The estimation of these errors is not simple and, therefore, the exact solution of the problem can not be obtained in most of the cases ((4.1)).