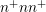Preface and Acknowledgement

This thesis summarizes my contributions to the enhancement of the spherical harmonics expansion (SHE) method developed during my doctoral studies. While microelectronics is at the heart of this thesis, it also touches on a number of related scientific fields: On the one hand, the ubiquitous solid-state physics provides the framework for all investigations of carrier transport in semiconductors, while on the other hand rather pure mathematics provides approximation results for the expansion of a function into spherical harmonics. In between, a considerable amount of scientific computing is also covered using the toolbox of modern programming paradigms. The latter is beyond the scope of this work and not further discussed, even though I consider it as one of the keys for extending the SHE method to three spatial dimensions.

The last three years consisted of a number of key events. I wish to reflect them in the following in order to also document the timeline that has lead to the hard scientific facts discussed in the remainder of this work. A discussion of whether luck, fate or something else was the main trigger for each of these events is beyond the scope of this thesis and thus left to the interpretation of the reader.

It all started in late 2008 with Prof. Tibor Grasser sending me a paper of Prof. Christoph Jungemann. Prof. Grasser was convinced that the SHE method is the ideal topic for a microelectronics-mathematics hybrid like myself. In retrospective, I am very glad that he has not mentioned at that time that other students had failed to achieve notable progress while working on the method. Consequently, the year 2009 was mostly devoted to making myself familiar with the existing literature and to summarizing my gained knowledge in a master’s thesis supervised by Prof. Ansgar Jüngel. Even though only one-dimensional 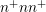-diodes were investigated numerically, first experiences with the peculiarities of the Boltzmann transport equation could already be gathered. Also, the mathematical focus led to first results on the coupling structure of the SHE equations.

In February 2010 I was given the chance to visit the group of Prof. Jungemann at the Bundeswehr University in Neubiberg, Munich. The first results on the coupling structure could be refined, yet my personal aim for the stay was to have a first implementation of a spatially two-dimensional SHE simulator ready when heading back to Vienna. This essentially required to restart from scratch and to come up with a two-dimensional drift-diffusion implementation in order to have a reasonable initial guess for the electrostatic potential. Moreover, an incomplete LU factorization preconditioner for the convergence of the iterative solvers had to be implemented. As a huge fan of winter sports, it required a lot of discipline to keep myself on coding in the evenings rather than watching the Olympic Winter Games, which were held in Vancouver during that time and thus broadcasted in Europe during the evening. The fruits of spending my time with my laptop and C++ instead of the television became visible on the last day of my stay, where the spatially two-dimensional simulation of a simple 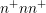-diode was completed. This paved the way for improvements on the SHE method in the months to come. I wish to thank Prof. Jungemann, Mr. Hong, Mr. Kovarik, Mr. Kraus, Mr. Matz, Mr. Thao and Mr. Dinh for hosting me in such a productive atmosphere.

It soon became apparent that a parallel preconditioner for SHE should be the next step. I could convince my colleague and friend Florian Rudolf (‘kleiner Meister’), who shares a lot of interest in programming graphics adapters with me, to work on a master’s thesis investigating the usefulness of OpenCL for general purpose computations on graphics adapters and multi-core central processing units. We spent two intensive weeks of implementing linear algebra, which after some final polishing resulted in the first release of ViennaCL. While the iterative solvers showed a speed-up of up to one order of magnitude compared to conventional single-threaded implementations, the incomplete LU factorization could not be accelerated properly due to its serial nature, thus prolongating the hunt for a parallel preconditioner for SHE.

During that time Josef Weinbub joined the development of ViennaCL. I could benefit a lot from his advanced knowledge of generic programming, which has entered ViennaCL on the one hand, and which also allowed me to reconsider the internals of the SHE simulator. Even though he had no direct contact with the SHE simulator and still considers it ‘evil witchcraft’, always leading to a smile on my face, he had a high influence on the coding style and design. I am deeply indebted for his indirect contributions, of which he may not be fully aware of.

Former experiences with finite element implementations and the now increased generic programming skills paired with experiences from subsequent ViennaCL releases led to the decision of a rigorous orthogonalization of software components in order to cope with the complexities of numerical methods in general and the SHE method in particular. It was clear to me that this decision required additional implementation effort at the beginning, but will pay off in the long run. At the end of 2010, ViennaData was essentially finished, and ViennaGrid reached a functional state in January 2011.

In February 2011, the combination of the individual software components ViennaCL for linear algebra, ViennaGrid for mesh management and ViennaData for the storage of quantities on mesh elements have all of a sudden lead to an enormous pace in the development of the SHE simulator ViennaSHE. Since the former three libraries have been tested and verified within other applications as well, ViennaSHE could be kept lightweight and with a focus on the algorithms specific to the SHE method only. This has reduced the time required for debugging to a bare minimum, simply because the amount of code in which a particular bug may show up was always very small and expressive. By the beginning of March, adaptive variable-order SHE as well as a parallel preconditioner were implemented and verified for a one-dimensional 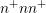-diode.

A little later in April, Prof. Grasser challenged me by asking for the possibility to extend ViennaSHE to unstructured grids and to extend the still brand-new adaptive variable orders and parallelization. Since this question was not new to me at that time, I replied that I expected the results from the one-dimensional evaluation to be transferable to spatially two-dimensional device simulations, hence it should work out. However, when he added that we should submit results for fully three-dimensional devices, I was very doubtful about this being possible given the other obligations I had until the deadline at the end of June. Instead of finding reasons why it definitely cannot be possible, I started with the required implementations. Without giving details about a race against time which ended 24 minutes before the extended deadline, I succeeded in submitting the results – and finally got accepted. Therefore, I wish to thank Prof. Grasser for continuously directing me in the right directions, and for being a positive example of a person who lives passion for science and his family.

I also wish to thank Prof. Ansgar Jüngel for his support and excitement whenever I reported new functionalities of ViennaSHE. In particular, he had been eagerly looking forward to full three-dimensional device simulations using the SHE method from the very beginning, hence I am very glad that it indeed all worked out. My thanks also go to Prof. Siegfried Selberherr, whose wide range of scientific sight and advise as well as his desire for highest quality I highly appreciate. Even though he is not my doctoral advisor, he always provided helpful guidance and plenty of valuable suggestions throughout my studies. I am also indebted to Prof. Erasmus Langer, who does a great job as head of the Institute for Microelectronics and cared for a fruitful environment especially during the financial crisis. I highly enjoyed sharing a room with Dr. Hajdin Ceric and Dr. Roberto Lacerda de Orio during the first half of my doctoral studies and wish to thank them for many interesting discussions. Markus Bina has been highly motivated and interested in joining the development of ViennaSHE from the day he joined the institute, but due to other obligations he had to restrict to verbally sharing his experiences with MinimosNT and giving advice on potential user requirements for ViennaSHE. I highly appreciate his input and look forward to the near future, which will finally allow him to actively join the development. In order to keep a reasonable scope of this preface, I collectively thank my co-workers at the Institute for Microelectronics and the Institute for Analysis and Scientific Computing for a respectful working environment.

A large amount of this thesis has been written at the Gasthof Schlagobersbauer in Alpl, Styria, home town of the Styrian poet Peter Rosegger. I express my gratitudes to Fam. Leitner, who ensured that I can fully focus on my writing. Nonetheless, the subsequent pages cannot compete with the literary excellence of Rosegger’s work.

The high level of motivation during my work on and around ViennaSHE would have been impossible without the deliberate and highly enjoyable distractions in the form of various gatherings and events with my friends, such as Neujahrs-LAN, birthday parties or evenings spent with cooking and/or sufficiently large amounts of exotic food. Thank you very much.

As a first quantum of return for unconditional support during my studies, I hope that my whole family can enjoy the completion of this thesis with me. In particular, and most importantly, I wish to thank Doris for her love and the tremendous amount of patience she offered throughout my studies.