D.1 Diabatic and Adiabatic Switching

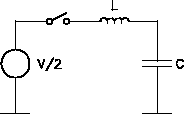
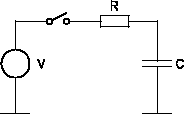
As laid out in Section 3.2 each time a capacitance is charged or discharged in a conventional circuit an energy of E = CV²/2 is dissipated, which is the dynamic contribution to the switching energy. The reason why this energy is dissipated is the so-called diabatic switching process, i.e., the electrical subsystem interacts with the thermal subsystem, allowing heat transfer. However, this is not necessarily the case. Especially, when a circuit contains only reactive elements capacitors can be charged and discharged at pleasure without any loss of energy.

The difference is shown in Fig. D.1, where a capacitance C is charged to a voltage V in two different ways.

Figure D.1: Charging and discharging a capacitor

[Diabatic]

[Adiabatic]

In the diabatic case the energy delivered by the voltage source is $V \int i d\!t = V Q = V^2 C$, but the energy stored in the capacitor is only V² C /2 no matter what the value of R is. The difference, V² C/2 is converted to thermal energy. In the adiabatic case, however, the source delivers only $V/2\, \int i d\!t = V/2\, Q = V^2 C/2$, ^D.2 which is just the energy transferred to the capacitor without any loss, provided the capacitor is ideal, i.e., lossless.

In a non-ideal circuit, however, capacitors are more or less lossy (most notably interconnections) and the switches have a finite turn-on resistance. In this case the charging of the capacitances has to be carried out in a finite time in order to keep the energy dissipation in the parasitic resistances down.

Figure D.2: Adiabatic charging in the presence of parasitic resistance

As shown in Fig. D.2 when the capacitor is charged at a rate of $V/\ensuremath{t_{\mathit{r}}}\xspace$ the current $I=CV/\ensuremath{t_{\mathit{r}}}\xspace$ flowing through the resistance R causes the dissipation of an energy

$$E_c = V^2C \frac{RC}{\ensuremath{t_{\mathit{r}}}\xspace } .$$ (D.1)

For example, to recover 99 percent of the stored energy the switching time must be 100 times the RC delay. Thus, the price to be paid for getting the energy back is speed.

Practically this means that the application of energy recovery is limited to special situations, where the ratio of $\ensuremath{t_{\mathit{r}}}\xspace /RC$ is affordable like, e.g., in the power supply and clocking of the chip or in drivers for external capacitive loads.

Footnotes

..., ^D.2

Note that the switch has to be closed for a time of $\ensuremath{t_{\mathit{r}}}\xspace =\pi/\sqrt{LC}$.