


 |  |  |
Digital computers cannot, in general, evaluate values with infinite precision and thus need to rely on approximations. It is, of course, among the goals of any scheme resulting in such an approximate value to have as little an error as possible. Numerical schemes to reduce this error, such as the Richardson extrapolation presented here, are therefore of great interest.
The Richardson extrapolation scheme assumes that a function 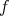 can be expanded around a point of
evaluation depending on a parameter
can be expanded around a point of
evaluation depending on a parameter 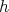 in a form
in a form
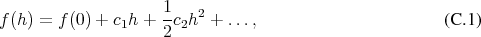
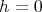 . Expanding the function at two
different values of the parameter
. Expanding the function at two
different values of the parameter 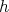 and
and 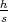 gives
gives
Multiplying Equation by  and subtracting Equation allows to eliminate the terms of order
and subtracting Equation allows to eliminate the terms of order
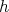
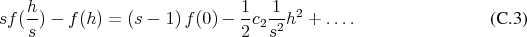
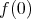 explicitly as
explicitly as
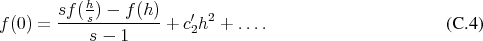
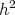 instead of the original order
instead of the original order 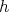 . This procedure can be applied
repeatedly to further increase the quality of the approximation.
. This procedure can be applied
repeatedly to further increase the quality of the approximation.
Applications using digital computers usually utilize factors  corresponding to powers of
corresponding to powers of  . This
allows the following settings
. This
allows the following settings
which further illustrate the recursive nature of the procedure.
 |  |  |