4.3.3 Total Scattering Rate

The fact that the dependence on the quasi-momentum enters (4.47) only through the dispersion law allows one to significantly simplify (4.14) using the Fermi golden rule [76]:

$$S(\vec{k},\vec{k}^{'})=\frac{V}{2\pi^{2}\hbar}\arrowvert V_\mathr... ...arrowvert^{2}\delta[\epsilon(\vec{k}^{'})-\epsilon(\vec{k})\pm \Delta\epsilon].$$ (4.47)

Making use of the delta function in the last expression (4.14) can be rewritten in the following manner:

$$\widetilde{\lambda}(\vec{k})=[1-f_\mathrm{FD}(\epsilon_{f})]\lambda(\vec{k})+f_\mathrm{FD}(\epsilon_{f})\lambda^{*}(\vec{k}),$$ (4.48)

where 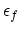$\epsilon_{f}$ denotes the final carrier energy 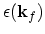$\epsilon(\vec{k}_{f})$. The backward scattering rate has been introduced as 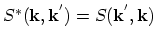$S^{*}(\vec{k},\vec{k}^{'})=S(\vec{k}^{'},\vec{k})$ and the total backward scattering rate as 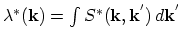$\lambda^{*}(\vec{k})=\int S^{*}(\vec{k},\vec{k}^{'})\,d\vec{k}^{'}$. (4.49) represents a linear combination of the forward and backward total scattering rates.

Figure 4.4: Schematic illustration of the scattering processes at high degeneracy.

In the non-degenerate case, 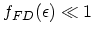$f_{FD}(\epsilon)\ll 1$, we obtain 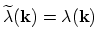$\widetilde{\lambda}(\vec{k})=\lambda(\vec{k})$ which means that scattering processes are mostly determined by the forward-scattering rate and thus the algorithm developed in [73] for non-degenerate statistics is restored. On the other hand, for highly degenerate semiconductors, 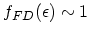$f_{FD}(\epsilon)\sim 1$, scattering processes are dominantly backward 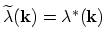$\widetilde{\lambda}(\vec{k})=\lambda^{*}(\vec{k})$. In the case of intermediate degeneracy both forward-scattering and backward-scattering contributes to the kinetics.

The fact that backward-scattering is dominant in processes where an initial state of an electron has lower energy than in its final state can formally be explained by the principle of detailed balance, given by the symmetry relation (see also (2.62))

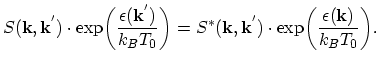$$S(\vec{k},\vec{k}^{'})\cdot\exp\biggl(\frac{\epsilon(\vec{k}^{'})... ...vec{k},\vec{k}^{'})\cdot\exp\biggl(\frac{\epsilon(\vec{k})}{k_{B}T_{0}}\biggr).$$ (4.49)

As can be seen from (4.50), forward transitions from high to low energy levels are preferred and backward transitions from low to high energy levels prevail.

It should be mentioned that at high degeneracy the backward scattering rate is dominant, and thus the probability of scattering to higher energy levels is larger than to lower energy levels as schematically shown in Fig. 4.4(a). Physically this means that lower energy levels are already occupied by particles, 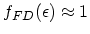$f_{FD}(\epsilon)\approx 1$ (see Fig. 4.4(b)) and, due to the Pauli exclusion principle, scattering to these energy levels is quantum mechanically forbidden.

S. Smirnov: