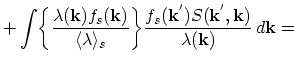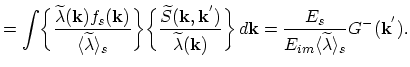To show the generation of the distributions 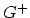 and
and 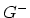 the integral representation of the stationary Boltzmann equation (4.10) is used.
First, the scattering operator in (4.10) is reformulated as:
the integral representation of the stationary Boltzmann equation (4.10) is used.
First, the scattering operator in (4.10) is reformulated as:
where the self-scattering rate
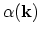 has been introduced. Note that the delta function guarantees that the self-scattering does not change an
electron state. Free-flight times are generated using the total scattering rate
has been introduced. Note that the delta function guarantees that the self-scattering does not change an
electron state. Free-flight times are generated using the total scattering rate
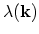 . Thus the self-scattering rate has to satisfy the
equality
. Thus the self-scattering rate has to satisfy the
equality
![$\displaystyle \lambda(\vec{k})=\int[1-f_{s}(\vec{k}^{'})]S(\vec{k},\vec{k}^{'})\,d\vec{k}^{'}+\alpha(\vec{k})\lambda(\vec{k}).$](img1032.png) |
(4.64) |
This gives for the self-scattering rate the following expression:
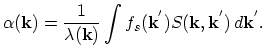 |
(4.65) |
Further, an additional differential scattering rate
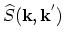 is introduced
is introduced
![$\displaystyle \widehat{S}(\vec{k},\vec{k}^{'})=[1-f_{s}(\vec{k}^{'})]S(\vec{k},\vec{k}^{'})+\alpha(\vec{k})\lambda(\vec{k})\delta(\vec{k}-\vec{k}^{'}),$](img1035.png) |
(4.66) |
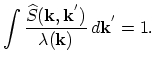 |
(4.67) |
Now taking into account (4.65) and (4.67) the scattering operator (4.64) takes the conventional form:
![$\displaystyle Q[f_{s}]=\int f_{s}(\vec{k}^{'})\widehat{S}(\vec{k}^{'},\vec{k})\,d\vec{k}^{'}-f_{s}(\vec{k})\lambda(\vec{k}).$](img1037.png) |
(4.68) |
Using the Neumann series of the forward equation the second iteration term (4.47) is derived as an example:
Here 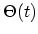 is the step function and
is the step function and
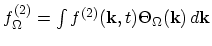 . From (4.71) it is seen that
if the free-flight time is calculated from the exponential distribution according to the scattering rate
. From (4.71) it is seen that
if the free-flight time is calculated from the exponential distribution according to the scattering rate
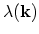 , the conditional probability
density for an after-scattering state
, the conditional probability
density for an after-scattering state
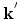 from the initial state
from the initial state 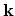 is equal to
is equal to
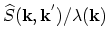 .
.
Within the algorithm presented in [82] the before-scattering distribution function is equal to
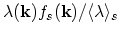 which gives the distribution
which gives the distribution 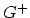 . In order to find the distribution function of the
after-scattering states the before-scattering distribution function should be multiplied by the conditional probability density for an after-scattering
state and this product is integrated over all before-scattering states. Using (4.67) and (4.66) one obtains for the
after-scattering distribution:
. In order to find the distribution function of the
after-scattering states the before-scattering distribution function should be multiplied by the conditional probability density for an after-scattering
state and this product is integrated over all before-scattering states. Using (4.67) and (4.66) one obtains for the
after-scattering distribution:
Note that the after-scattering distribution is normalized to unity. Now it is obvious that the initial distributions 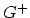 and
and 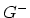 can be generated
by introduction the main trajectory which is constructed using the algorithm from [82] to solve (4.10). Then for each main
iteration two carrier ensembles with initial distributions
can be generated
by introduction the main trajectory which is constructed using the algorithm from [82] to solve (4.10). Then for each main
iteration two carrier ensembles with initial distributions 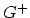 and
and 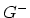 evolve in time according to (4.11) for the secondary
trajectories.
evolve in time according to (4.11) for the secondary
trajectories.
S. Smirnov:
![]() is introduced
is introduced
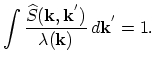
![$\displaystyle Q[f_{s}]=\int f_{s}(\vec{k}^{'})\widehat{S}(\vec{k}^{'},\vec{k})\,d\vec{k}^{'}-f_{s}(\vec{k})\lambda(\vec{k}).$](img1037.png)
![]() which gives the distribution
which gives the distribution ![]() . In order to find the distribution function of the
after-scattering states the before-scattering distribution function should be multiplied by the conditional probability density for an after-scattering
state and this product is integrated over all before-scattering states. Using (4.67) and (4.66) one obtains for the
after-scattering distribution:
. In order to find the distribution function of the
after-scattering states the before-scattering distribution function should be multiplied by the conditional probability density for an after-scattering
state and this product is integrated over all before-scattering states. Using (4.67) and (4.66) one obtains for the
after-scattering distribution:
![$\displaystyle \int\biggl\{\frac{\lambda(\vec{k})f_{s}(\vec{k})}{\langle\lambda\...
...frac{[1-f_{s}(\vec{k}^{'})]S(\vec{k},\vec{k}^{'})}{\lambda(\vec{k})}\,d\vec{k}+$](img1047.png)
![$\displaystyle +\frac{\lambda(\vec{k}^{'})f_{s}(\vec{k}^{'})}{\langle\lambda\ran...
...frac{[1-f_{s}(\vec{k}^{'})]S(\vec{k},\vec{k}^{'})}{\lambda(\vec{k})}\,d\vec{k}+$](img1048.png)