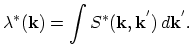(4.11) contains terms which depend on the stationary distribution function
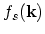 . These are the free term and the scattering term. The
stationary distribution function is the solution of (4.10). This fact prevents an analytical solution
for
. These are the free term and the scattering term. The
stationary distribution function is the solution of (4.10). This fact prevents an analytical solution
for
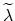 , and a numerical integration is necessary. However, in this work a rejection technique is applied to solve (4.11). In
Section 4.2.1 a new differential scattering rate
, and a numerical integration is necessary. However, in this work a rejection technique is applied to solve (4.11). In
Section 4.2.1 a new differential scattering rate
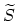 has been introduced (see (4.13)). Here another differential
scattering rate is defined according to the following expression:
has been introduced (see (4.13)). Here another differential
scattering rate is defined according to the following expression:
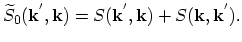 |
(4.71) |
The corresponding total scattering rate is
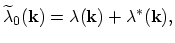 |
(4.72) |
where
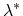 stands for the total backward-scattering rate
stands for the total backward-scattering rate
| |
|
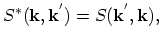 |
|
| |
|
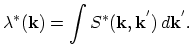 |
(4.73) |
From (4.13) and (4.72) it follows that
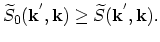 |
(4.74) |
To solve (4.11) a wave vector 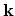 is generated using the differential scattering rate
is generated using the differential scattering rate
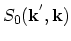 . The condition of
acceptance takes the following form
. The condition of
acceptance takes the following form
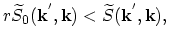 |
(4.75) |
where 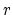 is a random number evenly distributed between 0 and
is a random number evenly distributed between 0 and 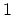 . The last inequality may be rewritten as follows:
. The last inequality may be rewritten as follows:
![$\displaystyle r[S(\vec{k}^{'},\vec{k})+S(\vec{k},\vec{k}^{'})]<(1-f_{s}(\vec{k}))S(\vec{k}^{'},\vec{k})+f_{s}(\vec{k})S(\vec{k},\vec{k}^{'}).$](img1060.png) |
(4.76) |
When the scattering process can be split into the sum of the emission and absorption of some quasi-particles such as
phonons and plasmons, this condition can be rewritten. Considering a forward transition from
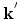 to
to 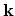 it can be easily shown that
one of the following rejection conditions has to be checked depending on whether an absorption or emission process has occurred. For absorption processes
it takes the form:
it can be easily shown that
one of the following rejection conditions has to be checked depending on whether an absorption or emission process has occurred. For absorption processes
it takes the form:
![$\displaystyle r[1+\frac{N_\mathrm{eq}}{N_\mathrm{eq}+1}]<[1-f_{s}(\vec{k})]\frac{N_\mathrm{eq}}{N_\mathrm{eq}+1}+f_{s}(\vec{k}),$](img1061.png) |
(4.77) |
whereas for emission processes the following condition is checked
![$\displaystyle r[1+\frac{N_\mathrm{eq}}{N_\mathrm{eq}+1}]<1-f_{s}(\vec{k})+f_{s}(\vec{k})\frac{N_\mathrm{eq}}{N_\mathrm{eq}+1},$](img1062.png) |
(4.78) |
where
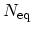 denotes the equilibrium number of quasi-particles. For example, when
denotes the equilibrium number of quasi-particles. For example, when
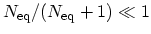 it follows from
(4.78) and (4.79) that for the non-degenerate case,
it follows from
(4.78) and (4.79) that for the non-degenerate case, 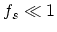 , emission processes will be dominantly accepted while absorption processes will
be mostly rejected. This means that the kinetic behavior is determined by emission processes. On the other side for the degenerate case, when
, emission processes will be dominantly accepted while absorption processes will
be mostly rejected. This means that the kinetic behavior is determined by emission processes. On the other side for the degenerate case, when
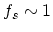 , it follows from the same relations that emission processes will be mostly rejected while the probability of the acceptance of absorption
processes increases. Finally, it should be noted that for elastic processes,
, it follows from the same relations that emission processes will be mostly rejected while the probability of the acceptance of absorption
processes increases. Finally, it should be noted that for elastic processes,
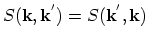 , the rejection condition
(4.77) takes the following form:
, the rejection condition
(4.77) takes the following form:
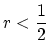 |
(4.79) |
This means that one half of the elastic scattering events will not be accepted in the rejection scheme given above.
S. Smirnov: