Next: 3. 2. 2 Edge-Based Boundary Integrals Up: 3. 2 Finite Volume Schemes Previous: 3. 2 Finite Volume Schemes
As a first step a function space
![]() is defined on the tessellated simulation domain. Typically, linear shape functions are assumed, however, it only has to be assured that all shape functions are continuous [58]. For the secondary graph simulation method only vertices and edges of the cell complex are used. Furthermore, the cell complex is associated its dual graph comprising the cells of the Voronoi tesselation as well as the boundary surfaces of these boxes. Dual elements of vertices are cells which cover the set of points closer to the respective vertex than to any other vertex [78]. Each edge is assigned a part of the boundary surface of the dual cell. If the original tesselation fulfills the Delauney property, a dual graph can be constructed in a unique manner and the cells are disjoint and bounded by the surfaces.
If the Delauney property holds true for a cell complex, each vertex
is defined on the tessellated simulation domain. Typically, linear shape functions are assumed, however, it only has to be assured that all shape functions are continuous [58]. For the secondary graph simulation method only vertices and edges of the cell complex are used. Furthermore, the cell complex is associated its dual graph comprising the cells of the Voronoi tesselation as well as the boundary surfaces of these boxes. Dual elements of vertices are cells which cover the set of points closer to the respective vertex than to any other vertex [78]. Each edge is assigned a part of the boundary surface of the dual cell. If the original tesselation fulfills the Delauney property, a dual graph can be constructed in a unique manner and the cells are disjoint and bounded by the surfaces.
If the Delauney property holds true for a cell complex, each vertex
![]() is assigned a dual cell
is assigned a dual cell
![]() . Consequently, an edge incident with the vertex
. Consequently, an edge incident with the vertex
![]() bounds the cell
bounds the cell
![]() .
.
Each local shape function is defined with respect to a vertex and is non-zero on all cells incident with this vertex. In the finite volume method, the governing differential operator
![]() has the form
has the form
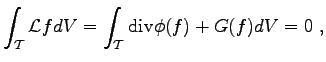 |
(3.21) |
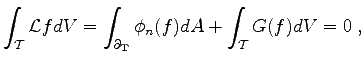 |
(3.22) |
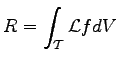 |
(3.23) |
 \; ,$](img290.png) |
(3.24) |
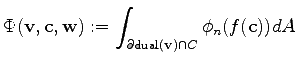 |
(3.25) |
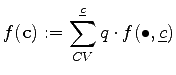 |
(3.26) |
Michael 2008-01-16