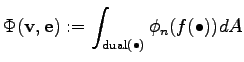3. 2. 2 Edge-Based Boundary Integrals
In the former section the integration domain of the dual cell of the vertex was separated cell-wise by
 \; .$](img295.png) |
(3.27) |
As a simplification of this method, the boundary surface can be written in the following manner:
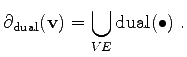 |
(3.28) |
This means that the surface can be written in terms of edges incident to a given vertex. The boundary integral can therefore be written as follows:
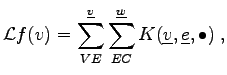 |
(3.29) |
Even though more traversal methods are required, the evaluation of the inner integral can be simplified, because the integration domain (surface) is a subset of a plane.
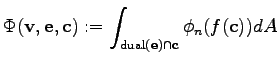 |
(3.30) |
Under the assumption that there is no change of the normal derivative throughout the surface element or - the weaker assumption - that the integral mean of the normal derivative throughout the surface element can be calculated by a point-to-point interpolation along the edge, shape functions only need to be explicitly defined on the edges whereas the function value on the cells themselves is not relevant for the calculations.
As a consequence, the integration of the functional 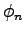 does not need to be performed explicitly for each part of the boundary of the dual cell of a vertex. In such a case only one mean value for the flux functional
does not need to be performed explicitly for each part of the boundary of the dual cell of a vertex. In such a case only one mean value for the flux functional 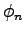 has to be determined and multiplied with the area of the surface part
has to be determined and multiplied with the area of the surface part 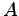 associated to the edge.
associated to the edge.
 = [\sum_{VE}^{\underline{v}} \Phi(\underline{v}, \bullet)](\mathbf{v})\;$](img300.png) |
(3.31) |
In this case the integral is evaluated on the complete surface part dual to the edge
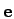 .
.
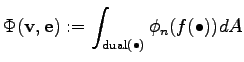 |
(3.32) |
Accordingly, the function passed to the functional 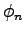 does not depend on the actual position on the surface and is therefore multiplied with the area of the surface in order to determine the flux. The integral can be cancelled and
does not depend on the actual position on the surface and is therefore multiplied with the area of the surface in order to determine the flux. The integral can be cancelled and 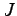 yields
yields
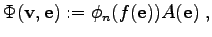 |
(3.33) |
where
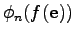 is evaluated on the point at the intersection of the edge and the surface element dual to the edge. This point is - due to the Delauney property - usually located in the middle between the bounding points of the edge.
is evaluated on the point at the intersection of the edge and the surface element dual to the edge. This point is - due to the Delauney property - usually located in the middle between the bounding points of the edge.
This formula is based on the assumption that the flux at the edge is representative for the whole surface and does not vary along the surface or the integral at the surface only depends on the flux at the edge. It is clear that this assumption can not be fulfilled for different kinds of shape functions, but for most of the cases such a condition is fulfilled approximately. For linear shape functions the condition is fulfilled exactly, because the tangential derivative between two neighboring elements is identical and the derivatives are constant throughout the cells.
In some cases, e.g. the shape functions for the Scharfetter Gummel discretization scheme [3] on a two-dimensional simulation domain, the shape functions are not defined at all for the elements. Moreover, it is assumed that there are sufficiently well behaved shape functions (which are not explicitly given) that fulfill the required properties approximately.
Michael
2008-01-16
 \; .$](img295.png)
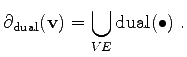
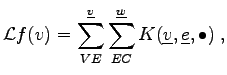
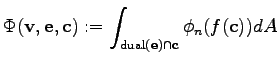
![]() does not need to be performed explicitly for each part of the boundary of the dual cell of a vertex. In such a case only one mean value for the flux functional
does not need to be performed explicitly for each part of the boundary of the dual cell of a vertex. In such a case only one mean value for the flux functional ![]() has to be determined and multiplied with the area of the surface part
has to be determined and multiplied with the area of the surface part ![]() associated to the edge.
associated to the edge.
 = [\sum_{VE}^{\underline{v}} \Phi(\underline{v}, \bullet)](\mathbf{v})\;$](img300.png)