3. 2. 5 Volume Integration

Hitherto, the boundary integrals have been discussed, while the integration of the terms $g$ was not mentioned at all. These integrals are usually on the associated dual cell of the vertex. In the following it is assumed that for the integration the functional $g$ has the form of a ($n$ -dimensional) Dirac pulse which is located in the geometrical point of the vertex.

Another method is to assume that the variable value is distributed uniformly on the cell. Even though such an interpretation of the quantity value is possible, it inevitably leads to an inconsistence: Given the Poisson equation, the functional $g$ is the cell-wise constant right hand side of the equation and does not depend on the function $f$ . If $g(f)$ is constant, the assumption of linear shape functions as chosen for the Laplace equation is inconsistent, because the Laplace operator applied to the shape function always yields zero.

Therefore, the integral is evaluated by multiplying the function value associated with the vertex with the volume of the dual cell of the vertex. If the functional $g$ depends on $f$ , e.g. $g = \sin(f)$ , the evaluation of the cell is more complicated and not further discussed here. In most of the cases it is appropriate to approximate $f = f(\mathbf{v})$ throughout the dual cell of $\mathbf{v}$ . Therefore, the following approximation can be derived:

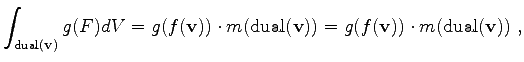$$\int_\mathbf{\mathrm{dual}(\mathbf{v})} g(F) dV = g(f(\mathbf{v})... ...m{dual}(\mathbf{v})) = g(f(\mathbf{v})) \cdot m(\mathrm{dual}(\mathbf{v})) \; ,$$ (3.37)

where the function $m$ denotes the volume of a given dual cell. For the sake of brevity, these two functions can be combined and one obtains the final formulation.

The distribution of quantities can be obtained from the topological view on the discretization scheme. All solution quantities which are required to form the solution function are associated with vertices. Furthermore, all quantities which are required to specify the function $g$ are associated with the vertex.

Geometrical quantities are associated with the topological elements or their dual elements for which they are required. As an example, the volume of a cell (finite volume) is assigned to the vertex which is dual to the respective cell. The area of the dual surface of an edge is stored as an edge-based quantity. The length of an edge is also stored as edge-based quantity.