Next: 3. 3. 2 Implementation-Based Formulation Up: 3. 3 Boundary Element Method Previous: 3. 3 Boundary Element Method
In contrast to finite elements or finite volumes, shape functions do not have local support but they are non-zero throughout the simulation domain. Normally, basis functions are defined in a manner that they are defined by functions having boundary facets as local support. These facets are incident with a common vertex. In the two-dimensional case, the facets are (boundary) edges incident with a boundary vertex.
The typical formulation of a boundary element scheme can be written in the following manner (Galerkin formulation)
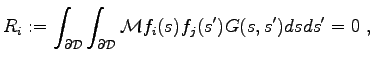 |
(3.46) |
| (3.47) |