Next: 3. 3. 3 Conclusion Up: 3. 3 Boundary Element Method Previous: 3. 3. 1 Standard Formulation
The outer integral along the boundary of the simulation domain can be simplified in the following manner by assuming the local support of the basis function:
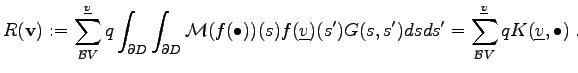 |
(3.49) |
|
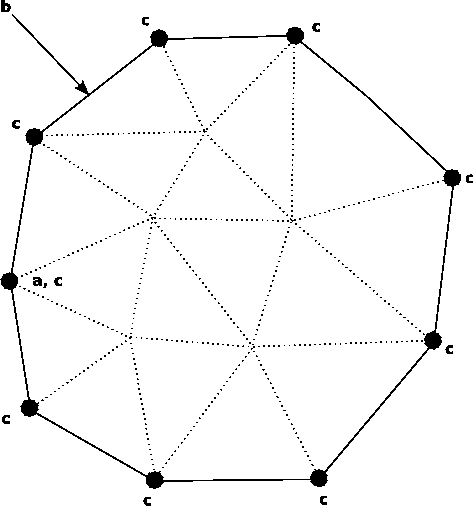
The integral expression depends on the type of weighting functions and the shape functions. In this case the Galerkin method is used which means that the shape functions and the weighting functions are equal. Furthermore, the integral expression depends on the choice of the boundary conditions used. Figure 3.9 shows the topological dependences and requirements for the implementation of the boundary element discretization scheme. For the implementation the topological incidence function
![]() is required. Due to the linearity of the boundary condition, the formulation can be re-written in the following form, where the coefficients
is required. Due to the linearity of the boundary condition, the formulation can be re-written in the following form, where the coefficients ![]() and
and ![]() can be extracted by treating the expressions
can be extracted by treating the expressions ![]() and
and
![]() of (3.48) separately.
of (3.48) separately.