In the following section it is assumed that the thermal capacitance 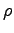 depends on the temperature of the respective material. In analogy a nonlinear dependence of the thermal conductance
depends on the temperature of the respective material. In analogy a nonlinear dependence of the thermal conductance 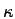 with respect to the temperature can be specified. However, for the sake of simplicity the heat conductance
with respect to the temperature can be specified. However, for the sake of simplicity the heat conductance 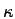 is assumed to be constant in the following example.
is assumed to be constant in the following example.
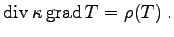 |
(4.18) |
A finite volume discretization yields for the same four-point geometry as in the linear example of the last section:
By inserting the neighborhood information and setting the thermal generation term 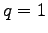 and
and
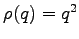 , the following expression is obtained.
, the following expression is obtained.
When using the Newton method it is always assumed that a given (already good) result is used to obtain a better result (see Fig. ![[*]](crossref.png) ). For the linear problem, a Newton scheme leads to a solution within one single step, because all higher-order terms vanish. For this reason in the linear case the choice of an initial guess does not play a role.
). For the linear problem, a Newton scheme leads to a solution within one single step, because all higher-order terms vanish. For this reason in the linear case the choice of an initial guess does not play a role.
Figure:
The solutions of the linearized problems converge to the solution of the nonlinear problem using the Newton method.
|
|
For the nonlinear case, it is however important to chose a proper initial guess. In the following, the initial values
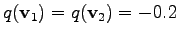 is chosen. Therefore, the expressions
is chosen. Therefore, the expressions
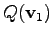 and
and
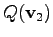 yield
yield
![$\displaystyle Q(\mathbf{v}_1) := [1, 0; -0.2]$](img485.png) |
|
![$\displaystyle Q(\mathbf{v}_2) := [0, 1; -0.2]$](img486.png) |
(4.20) |
First, the application of the
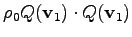 is performed as follows
is performed as follows
![$\displaystyle Q(\mathbf{v}_1) \cdot T_1 = [1, 0; -0.2] \cdot [1, 0; -0.2] =$](img488.png) |
|
![$\displaystyle Q(\mathbf{v}_1) \cdot [-0.4, 0; 0.04] = \cdot [-0.4, 0; 0.04]$](img489.png) |
(4.21) |
Repeated application of this step (eventually) leads to a solution of this equation system. However, it has to be considered that nonlinear methods have different rates of convergence and sometimes solutions can not be found at all [82]. Nevertheless, the presented method with linearized expressions can be used for the formulation of all kinds of nonlinear problems, the solution of these problems can be treated separately from the assembly.
Michael
2008-01-16
![]() depends on the temperature of the respective material. In analogy a nonlinear dependence of the thermal conductance
depends on the temperature of the respective material. In analogy a nonlinear dependence of the thermal conductance ![]() with respect to the temperature can be specified. However, for the sake of simplicity the heat conductance
with respect to the temperature can be specified. However, for the sake of simplicity the heat conductance ![]() is assumed to be constant in the following example.
is assumed to be constant in the following example.
![[*]](crossref.png) ). For the linear problem, a Newton scheme leads to a solution within one single step, because all higher-order terms vanish. For this reason in the linear case the choice of an initial guess does not play a role.
). For the linear problem, a Newton scheme leads to a solution within one single step, because all higher-order terms vanish. For this reason in the linear case the choice of an initial guess does not play a role.
![\includegraphics[width=5cm]{DRAWINGS/nonlinear.eps}](img481.png)
![]() is chosen. Therefore, the expressions
is chosen. Therefore, the expressions
![]() and
and
![]() yield
yield