Next: 4. 1. 8 Refinement of Models Up: 4. 1 Line-Wise Assembly Previous: 4. 1. 6 Example - Nonlinear Conductivity
The discussed equations form a linear equation system whose solution vector gives an increment or update for the respective solution quantities. In the Newton scheme an equation system
![]() is linearized in the neighborhood of a vector
is linearized in the neighborhood of a vector
![]() of quantity values for
of quantity values for ![]() .
.
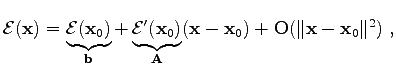 |
(4.24) |
For the first order case, the evaluation of the residuum in the respective linearization vector
![]() results in the (inverse) right hand side. The evaluation of the derivatives
results in the (inverse) right hand side. The evaluation of the derivatives
![]() in the linearization vector
in the linearization vector
![]() yields the entries of the system matrix.
yields the entries of the system matrix.
From this point of view, it can be stated that forming the derivatives from the discretized expression is performed implicitly when using linearized expressions. This is of course evident, when the Taylor expansion is considered, however, a lot of work for the differentiation of the respective equations can be saved. It also has to be stated that using this method for forming the derivatives only determines the derivative only for a given linearization vector
![]() and not an analytic expression. This implies that such a method is not apt for the differentiation of general algebraic formulae, however, it performs well for the specific matter.
and not an analytic expression. This implies that such a method is not apt for the differentiation of general algebraic formulae, however, it performs well for the specific matter.
Michael 2008-01-16