The use of linearized expressions can also be generalized so as to be employed for the specification of eigenvalue equations. In this case, expressions of the form
 the linearized expression can be specified. The Schrödinger equation which is typically used for the solution of quantum mechanical problems is a basic example for the treatment of eigenvalue equations using linear expressions.
the linearized expression can be specified. The Schrödinger equation which is typically used for the solution of quantum mechanical problems is a basic example for the treatment of eigenvalue equations using linear expressions.
Figure4.3:
The eigenvalue problem is specified on a four point one-dimensional equi-distant domain, where the two boundary points are set to zero. Two eigenvectors are shown.
|
|
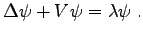 |
(4.25) |
The eigenvalue equation system can be written in the following line-wise form:
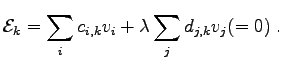 |
|
|
(4.26) |
For the sake of simplicity and in order to obtain a consistent short and concise notation comparable to linearized expressions (4.9), the following scheme is introduced:
![$\displaystyle \sum_i c_i v_i + \lambda \sum_j d_j v_j =: [c_1, \ldots, c_N ; d_1, \ldots, d_N ]$](img499.png) |
|
|
(4.27) |
As these eigenvalue equations are always linear, only linear operations have to be considered and a linear space is obtained.
![$\displaystyle [c_1, \ldots, c_N ; d_1, \ldots, d_N ] + [e_1, \ldots, e_N ; f_1, \ldots, f_N ] =$](img500.png) |
|
![$\displaystyle [c_1+e_1, \ldots, c_N+e_N ; d_1+f_1, \ldots, d_N+f_N ]$](img501.png) |
(4.28) |
![$\displaystyle [c_1, \ldots, c_N ; d_1, \ldots, d_N ] - [e_1, \ldots, e_N ; f_1, \ldots, f_N ] =$](img502.png) |
|
![$\displaystyle [c_1-e_1, \ldots, c_N-e_N ; d_1-f_1, \ldots, d_N-f_N ]$](img503.png) |
(4.29) |
![$\displaystyle a \cdot [c_1, \ldots, c_N ; d_1, \ldots, d_N ] =$](img504.png) |
|
![$\displaystyle [a \cdot c_1, \ldots, a \cdot c_N ; a \cdot d_1, \ldots, a \cdot d_N ]$](img505.png) |
(4.30) |
![$\displaystyle \lambda([c_1, \ldots, c_N ; 0, \ldots, 0 ]) = [0, \ldots, 0 ; c_1, \ldots, c_N ]$](img506.png) |
(4.31) |
An algebraic structure which introduces linear(ized) expressions to eigenvalue- expressions has to provide the following elements:
![$\displaystyle \mathrm{hom}([c_1, \ldots, c_N ; q]) = [c_1, \ldots, c_N ; 0, \ldots, 0 ]$](img507.png) |
|
|
(4.32) |
![$\displaystyle \lambda([c_1, \ldots, c_N ; q]) = [0, \ldots, 0 ; c_1, \ldots, c_N ]$](img508.png) |
|
|
(4.33) |
The following discretization is obtained in a one-dimensional simulation domain according to Figure 4.1 comprising four vertices when using finite differences. The solution is referred to as 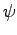 which is stored in the quantity
which is stored in the quantity 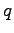 . In analogy to (4.12), the term
. In analogy to (4.12), the term 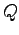 is introduced.
is introduced.
The potential is assigned constant values
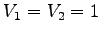 . For the probability function
. For the probability function 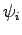 the following term is inserted
the following term is inserted
Accordingly, one obtains the following eigenvalue expressions:
In analogy to linearized expressions, linear eigenvalue expressions can be used in order to fill the eigenvalue matrices. One often observes that the matrix 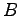 is the unit matrix. Often it is necessary to change the order of the equations in order to maintain the unit matrix for
is the unit matrix. Often it is necessary to change the order of the equations in order to maintain the unit matrix for 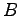 .
.
Michael
2008-01-16
![]() the linearized expression can be specified. The Schrödinger equation which is typically used for the solution of quantum mechanical problems is a basic example for the treatment of eigenvalue equations using linear expressions.
the linearized expression can be specified. The Schrödinger equation which is typically used for the solution of quantum mechanical problems is a basic example for the treatment of eigenvalue equations using linear expressions.
![\includegraphics[width=5cm]{DRAWINGS/eigen1.eps}](img495.png)
![\includegraphics[width=5cm]{DRAWINGS/eigen2.eps}](img496.png)
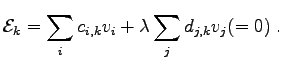
![$\displaystyle \sum_i c_i v_i + \lambda \sum_j d_j v_j =: [c_1, \ldots, c_N ; d_1, \ldots, d_N ]$](img499.png)